机器学习基础——梯度下降法（Gradient Descent）

看了coursea的机器学习课，知道了梯度下降法。一开始只是对其做了下简单的了解。随着内容的深入，发现梯度下降法在很多算法中都用的到，除了之前看到的用来处理线性模型，还有BP神经网络等。于是就有了这篇文章。

本文主要讲了梯度下降法的两种迭代思路，随机梯度下降（Stochastic gradient descent）和批量梯度下降（Batch gradient descent）。以及他们在python中的实现。

梯度下降法

梯度下降是一个最优化算法，通俗的来讲也就是沿着梯度下降的方向来求出一个函数的极小值。那么我们在高等数学中学过，对于一些我们了解的函数方程，我们可以对其求一阶导和二阶导，比如说二次函数。可是我们在处理问题的时候遇到的并不都是我们熟悉的函数，并且既然是机器学习就应该让机器自己去学习如何对其进行求解，显然我们需要换一个思路。因此我们采用梯度下降，不断迭代，沿着梯度下降的方向来移动，求出极小值。

此处我们还是用coursea的机器学习课中的案例，假设我们从中介那里拿到了一个地区的房屋售价表，那么在已知房子面积的情况下，如何得知房子的销售价格。显然，这是一个线性模型，房子面积是自变量x，销售价格是因变量y。我们可以用给出的数据画一张图。然后，给出房子的面积，就可以从图中得知房子的售价了。

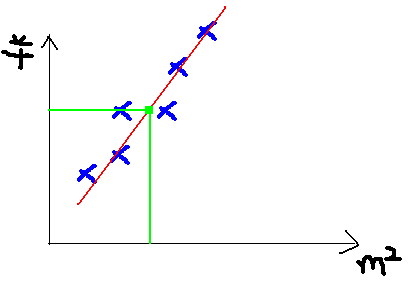
现在我们的问题就是，针对给出的数据，如何得到一条最拟合的直线。

对于线性模型，如下。

• h(x)是需要拟合的函数。
• J(θ)称为均方误差或cost function。用来衡量训练集众的样本对线性模式的拟合程度。
• m为训练集众样本的个数。
• θ是我们最终需要通过梯度下降法来求得的参数。

\[h(\theta)=\sum_{j=0}^n \theta_jx_j \\
J(\theta)=\frac1{2m}\sum_{i=0}^m(y^i-h_\theta(x^i))^2\]

接下来的梯度下降法就有两种不同的迭代思路。

批量梯度下降（Batch gradient descent）

现在我们就要求出J(θ)取到极小值时的\(θ^T\)向量。之前已经说过了，沿着函数梯度的反方向下降就能最快的找到极小值。

1. 计算J(θ)关于\(\theta^T\)的偏导数,也就得到了向量中每一个\(\theta\)的梯度。

\[\begin{align}
\frac{\partial J(\theta)}{\partial\theta_j}
& = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i)) \\
& = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_jx_j^i-y^i) \\
& = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j
\end{align}
\]

1. 沿着梯度的反方向更新参数θ的值

\[\theta_j := \theta_j + \alpha\frac{\partial J(\theta)}{\partial\theta_j}
:=\theta_j - \alpha\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i))x^i_j
\]

1. 迭代直到收敛。
   
   
   
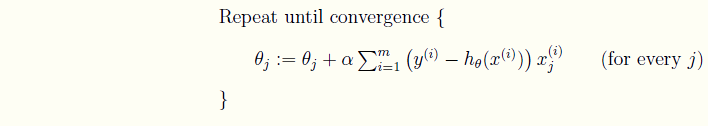
   可以看到，批量梯度下降是用了训练集中的所有样本。因此在数据量很大的时候，每次迭代都要遍历训练集一遍，开销会很大，所以在数据量大的时候，可以采用随机梯度下降法。

随机梯度下降（Stochastic gradient descent）

和批量梯度有所不同的地方在于，每次迭代只选取一个样本的数据，一旦到达最大的迭代次数或是满足预期的精度，就停止。

可以得出随机梯度下降法的θ更新表达式。

\[\theta_j:=\theta_j - \alpha\frac1m(y^i-h_\theta(x^i))x^i_j
\]

迭代直到收敛。

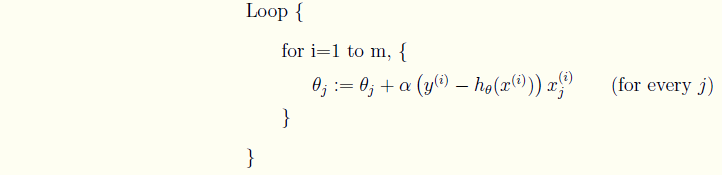
两种迭代思路的python实现

下面是python的代码实现，现在仅仅是用纯python的语法（python2.7）来实现的。随着学习的深入，届时还会有基于numpy等一些库的实现，下次补充。

#encoding:utf-8

#随机梯度
def stochastic_gradient_descent(x,y,theta,alpha,m,max_iter):
	"""随机梯度下降法，每一次梯度下降只使用一个样本。

	:param x: 训练集种的自变量
	:param y: 训练集种的因变量
	:param theta: 待求的权值
	:param alpha: 学习速率
	:param m: 样本总数
	:param max_iter: 最大迭代次数
	"""
	deviation = 1
	iter = 0
	flag = 0
	while True:
		for i in range(m):	#循环取训练集中的一个
			deviation = 0
			h = theta[0] * x[i][0] + theta[1] * x[i][1]
			theta[0] = theta[0] + alpha * (y[i] - h)*x[i][0]
			theta[1] = theta[1] + alpha * (y[i] - h)*x[i][1]

			iter = iter + 1
			#计算误差
			for i in range(m):
				deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
			if deviation <EPS or iter >max_iter:
				flag = 1
				break
		if flag == 1 :
			break
	return theta, iter

#批量梯度
def batch_gradient_descent(x,y,theta,alpha,m,max_iter):
	"""批量梯度下降法，每一次梯度下降使用训练集中的所有样本来计算误差。

	:param x: 训练集种的自变量
	:param y: 训练集种的因变量
	:param theta: 待求的权值
	:param alpha: 学习速率
	:param m: 样本总数
	:param max_iter: 最大迭代次数
	"""
	deviation = 1
	iter = 0
	while deviation > EPS and iter < max_iter:
		deviation = 0
		sigma1 = 0
		sigma2 = 0
		for i in range(m): #对训练集中的所有数据求和迭代
			h = theta[0] * x[i][0] + theta[1] * x[i][1]
			sigma1 = sigma1 +  (y[i] - h)*x[i][0]
			sigma2 = sigma2 +  (y[i] - h)*x[i][1]
		theta[0] = theta[0] + alpha * sigma1 /m
		theta[1] = theta[1] + alpha * sigma2 /m
		#计算误差
		for i in range(m):
			deviation = deviation + (y[i] - (theta[0] * x[i][0] + theta[1] * x[i][1])) ** 2
		iter = iter + 1
	return theta, iter

#运行 为两种算法设置不同的参数
# data and init
matrix_x = [[2.1,1.5],[2.5,2.3],[3.3,3.9],[3.9,5.1],[2.7,2.7]]
matrix_y = [2.5,3.9,6.7,8.8,4.6]
MAX_ITER = 5000
EPS = 0.0001 

#随机梯度
theta = [2,-1]
ALPHA = 0.05

resultTheta,iters = stochastic_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters

#批量梯度
theta = [2,-1]
ALPHA = 0.05

resultTheta,iters = batch_gradient_descent(matrix_x, matrix_y, theta, ALPHA, 5, MAX_ITER)
print 'theta=',resultTheta
print 'iters=',iters

代码见github。https://github.com/maoqyhz/machine_learning_practice.git

运行结果

ALPHA = 0.05

theta= [-0.08445285887795494, 1.7887820818368738]
iters= 1025
theta= [-0.08388979324755381, 1.7885951009289043]
iters= 772
[Finished in 0.5s]

ALPHA = 0.01

theta= [-0.08387216503392847, 1.7885649678753883]
iters= 3566
theta= [-0.08385924864202322, 1.788568071697816]
iters= 3869
[Finished in 0.1s]

ALPHA = 0.1

theta= [588363545.9596066, -664661366.4562845]
iters= 5001
theta= [-0.09199523483489512, 1.7944581778450577]
iters= 516
[Finished in 0.2s]

总结

梯度下降法是一种最优化问题求解的算法。有批量梯度和随机梯度两种不同的迭代思路。他们有以下的差异：

• 批量梯度收敛速度慢，随机梯度收敛速度快。
• 批量梯度是在θ更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个样本来更新的
• 批量梯度的开销大，随机梯度的开销小。

使用梯度下降法时需要寻找出一个最好的学习效率。这样可以使得使用最少的迭代次数达到我们需要的精度。

参考文献

• 在博客中使用LaTeX插入数学公式
• 随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）的公式对比、实现对比
• 随机梯度下降法
• 线性回归与梯度下降算法
• 梯度下降算法的Python实现