DAY 3 数论专场

2019-07-23

今天的题目一个比一个神仙，很早之前就在讨论今天是不是晚上回宾馆就没脑子了，后来发现，是中午。。。。

一上午就讲了一个PPT，然而标题就两个子---数论。。。

这谁顶的住。。。。
整除和剩余：

上来什么都没说直接就是同余，讲了一堆公式和证明，回宾馆发现，证明一个不会。。。。

素数：

讲了好多筛法，发现只会一个埃筛就够用了。。。。

然后就发现了一个O(n)的筛法

 int not_prime[N],prime[N],count;
 for(int i=;i<=n;i++)
 {
     if(!not_count[i])
     {
         prime[++count]=i;
     }
     for(int j=;j<=count;j++)
     {
         if(prime[j]*i>N)
         {
             break;
         }
         not_prime[i*prime[j]]=true;
         if(i%prime[j]==)
         {
             break;//不好理解，如果这个数不是个素数，且当它的最小素数因子为p[j]时，停止循环（只将排在最小素数因子之前的素数与其相乘，判断出其合数，往后不执行，因为一个数是两个素数的积的话，总会有一个素数在排除其倍数时把此数的倍数一并排除掉）
         }
     }
 }//欧拉筛

然后就讲了欧拉函数，然后就讲了一堆证明，然后就GG了。。。。

欧拉定理：

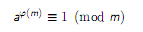
然后就是广义欧拉定理，发现将和不讲好像没区别。。。。

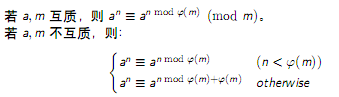
线性同余方程：

欧几里得算法：

GCD（a，b）=GCD（b，a-b）

然后就是逆元什么的。。。。

高次不等式：

老师说没时间讲了，就自己看看吧，然后发现一点都看不懂。。。

组合数学

这个东西莫名想到了前一段时间物理老师天天说的东西。。。。

二项式定理：

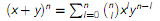
这个东西感觉高考好像还考，前一段时间做习题狂做还看到过。。。

Lucas定理：

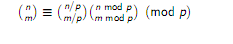
莫名想吐槽一下，老师是先讲的EXLucas。。。。

斯特林数：

老师没说，但还是想吐槽一下，机房大佬竟然都过了，还是一遍过！！！！四道题啊，那个阿基米德的澡盆就是公认的斯特林王。。。。

期望概率、

这个听得一脸蒙还是要回去看看。

线性代数

本以为会讲很高深的东西，后来发现就讲了矩阵快速幂，还是那熟悉的斐波那契，还是那毒瘤的p4000。

但今天跟着北大的高材生学会了压行。。。。

2019-07-23