GCN python 实现2：利用GCN进行节点分类

参考：https://www.baidu.com/link?url=5oU-O_YQV8DdSTtRkgzsQ_vuwjJHyUOxqeAKhq98ZA5XtvKW8PNQwXgSlr5GpESRqhsMinCYR8O7nVh2zY125a&wd=&eqid=a487a7b100077ce3000000065d9eae75

图是信息的最佳表示方式。在一个图中，有通过边（谓之“关系”）连接起来的节点（谓之“实体”）。想一想，你的Facebook社交网络是个什么样子的：以你为中心连接上你的朋友们，他们又以不同的方式相互联系。在表格中表示这些信息的方式是有些随意（或者不好的），社交关系并不是像一排排规矩的摆在桌子上的东西，而是：

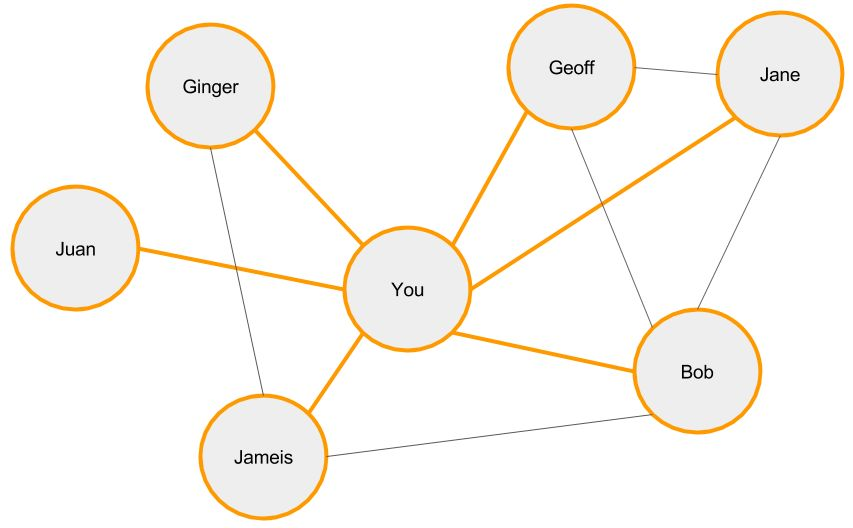
预测节点属性
现在我们得到了Facebook社交网络的最佳表示，那么如何去更好的预测你朋友们的喜好呢？
我们这里使用图卷积神经网络（Graph convolutional networks），GCN是一种新的深度学习架构，能够利用包含在数据以及数据之间关系中的信息。

来看一个例子，假设我们想要了解你的朋友们谁倾向于共和党派谁倾向于民主党派，我们将在Facebook 社交网络图上应用GCN，并将预测的“政治立场”这个节点属性分配给图中缺少标签的节点。
GCN网络有两个输入：首先需要列出你每个朋友的特征，包括母校、邮政编码、所属团体等等信息，很显然，这些信息是学习一个人政治倾向的特征；
第二，GCN采用图结构的精简形式，这帮助GCN学习朋友的友谊是如何影响他们的政治立场的。 按理说，仅这两条信息就足以预测一个人的政治倾向了。传统的深度学习模型甚至不需要应用实体之间的关系来进行预测，它们只利用个人属性。但是通过在GCN中结合数据的属性以及结构，可以使预测更加强大。

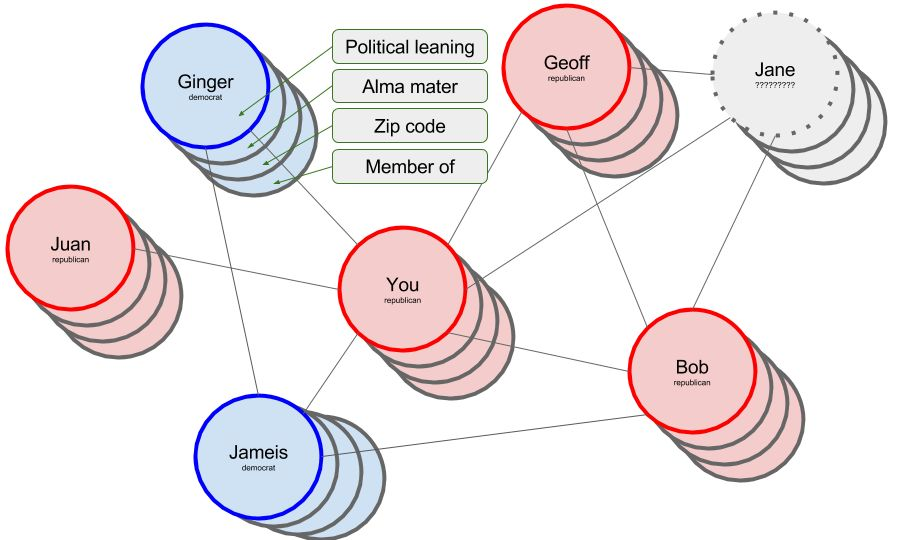
GCN的输入：Jane和很多共和党人有联系，但是她也有自己的一些属性，比如教育、地理位置，很多Facebook团体成员，那她到底是共和党派还是民主党派呢？

GCN的应用十分简单。它们是分层操作的，可以将它们堆叠在一起，达到想要的深度。在每一层的内部，有三个特点：
第一 标准化的图结构； 第二 标准化的图结构乘以节点属性； 第三 我们将非线性函数应用于节点属性和权重；

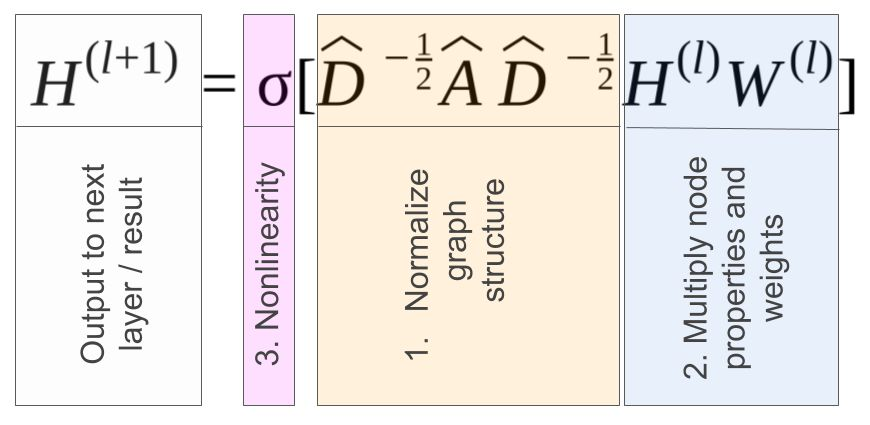
一个图卷积层，敏锐的读者会注意到，由于核函数的平稳性，这是一个近似卷积算子

在应用中，额外添加dropout层，激活函数采用Leaky ReLU，损失函数采用softmax loss，如下图所示：

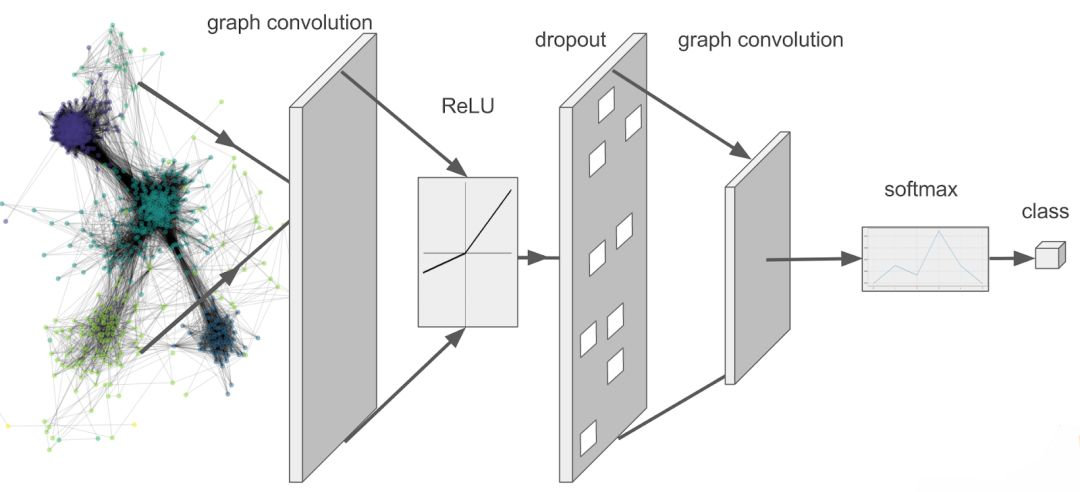
一个使用中间dropout层的双层图卷积神经网络，我发现leaky ReLU函数能够有助于缓解梯度消失。

我们来看一部分使用Tensorflow实现GCN层的代码，了解一下该网络设计的简单性。

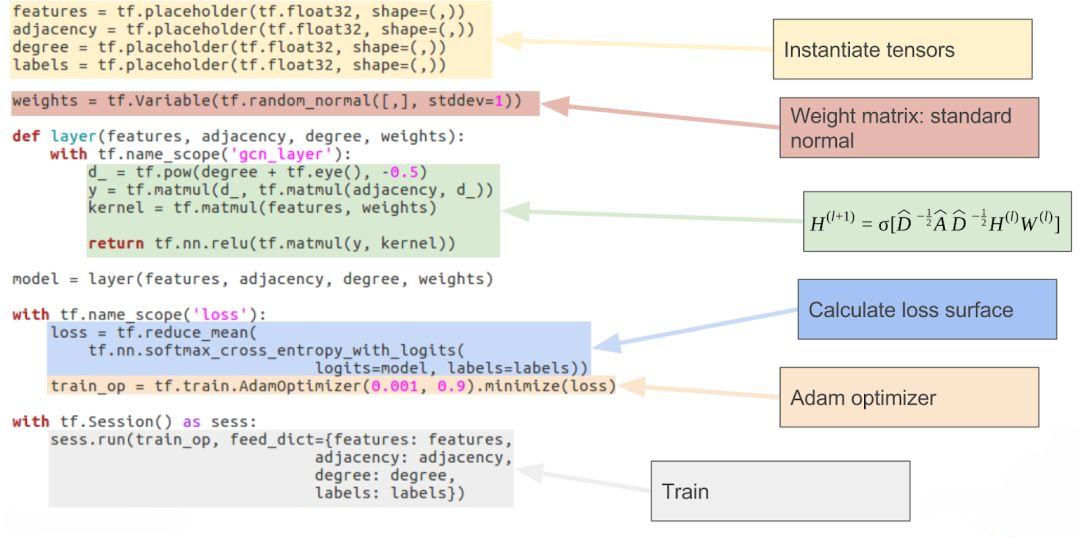
一个基于TensorFlow实现的图卷积神经网络，使用ADAM优化器，softmax交叉熵损失函数。绿色部分是图卷积层的实现，注意它的简洁。

应用 上面的例子太简单，无法证明该问题的复杂性。下面，我们看一个真正的Facebook网络，不同政治倾向的颜色不同。

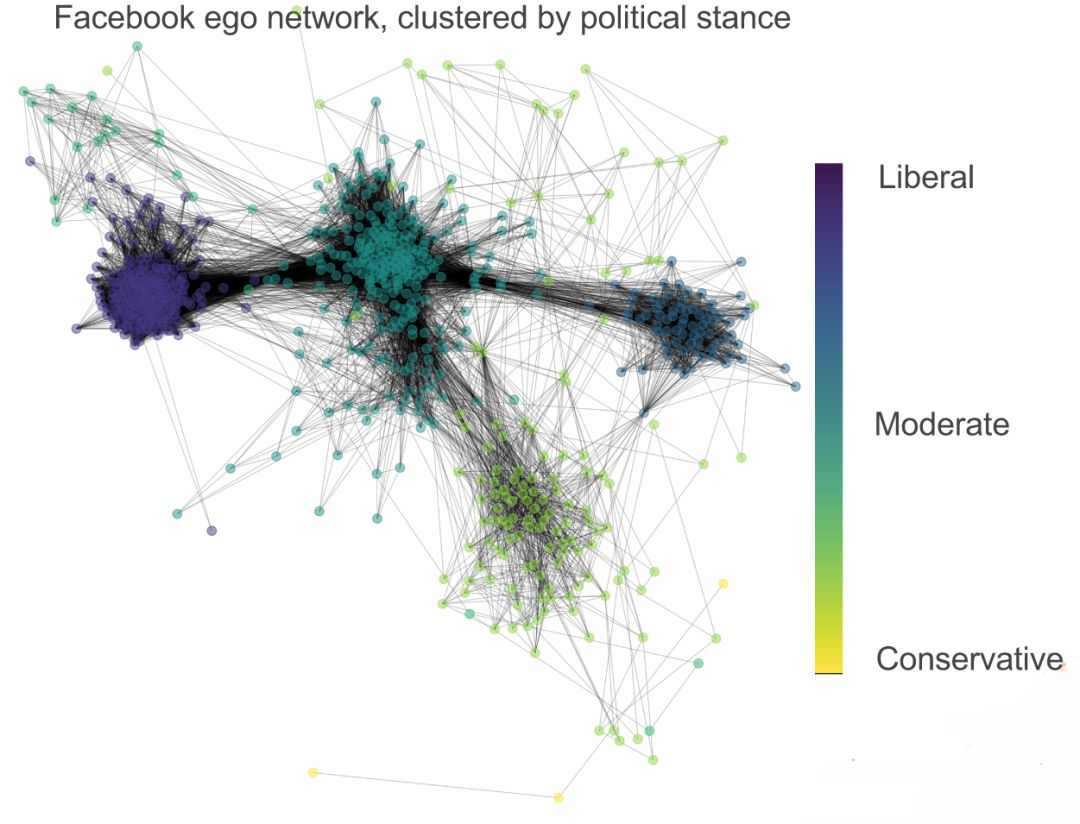
一个基于Facebook数据的网络，不同的颜色代表每个人不同的政治倾向，图卷积预测了10%的这些人的政治立场，其余的作为训练序列的一部分输入。 记住，GCN不在乎每个节点的输入数据，或者节点之间的关系是什么样的。我们可以任意使用数据，比如企业之间的金融交易数据和企业自身的财务状况信息，便可以使用GCN来告诉我们哪些交易具有欺诈性。建立一个企业的超级节点图，我们可以利用GCN找出洗钱团伙。

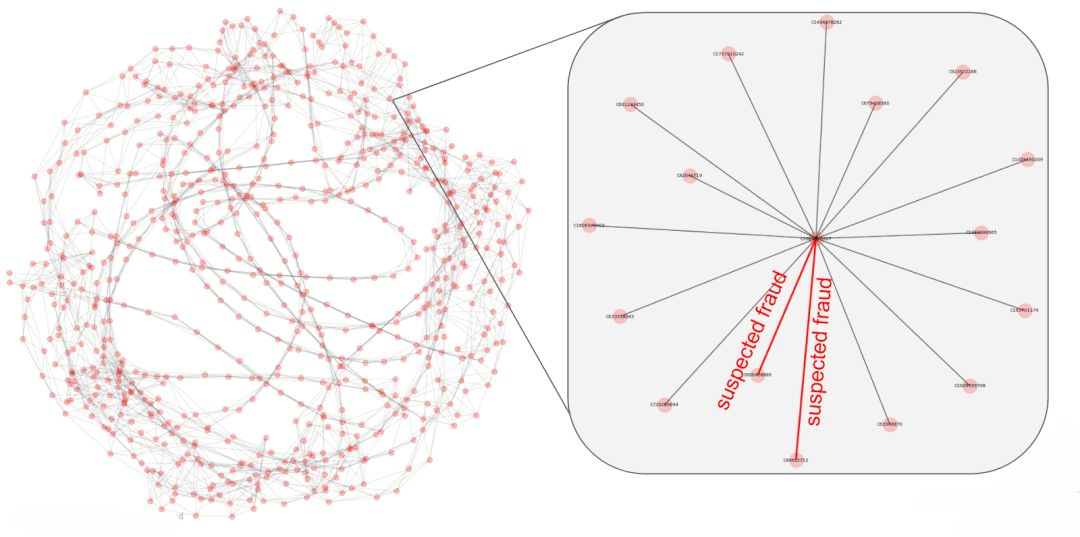
一个交易的超级节点图。这些组织中有没有洗钱圈？利用GCN找出违法分子。

我们可以将GCN应用到银行客户信用风险评估，根据客户的特征以及风险阈值找出哪些客户是不能审批贷款的。还可以利用历史银行数据。
利用数据的自然结构提高了机器学习的预测能力，因此认识到图的普遍性是非常重要的。每个企业每天都在处理很多数据，而这些数据非常适合用图结构来表示。在任何信息连接的情况下都会出现图相关的问题，任何有图的地方，背后都有惊人的价值等待被挖掘。