最小生成树——Kruskal与Prim算法

最小生成树——Kruskal与Prim算法

序：

首先：

啥是最小生成树？？？

咳咳。。。

如图：

在一个有n个点的无向连通图中，选取n-1条边使得这个图变成一棵树。这就叫“生成树”。（如下图）

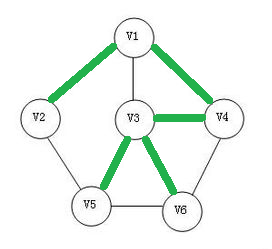
每个无向连通图都会拥有至少一个生成树。

而在无向连通图中，我们让每一个边都拥有一个边权（就是每个边代表一个值）。

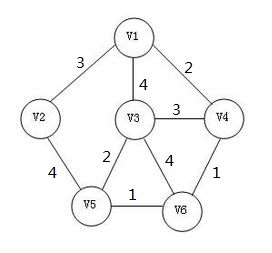
而我们在有边权的无向连通图中构造一个生成树，使得这个生成树所用的边的边权之和最小。这个生成树就叫这个无向连通图的最小生成树！

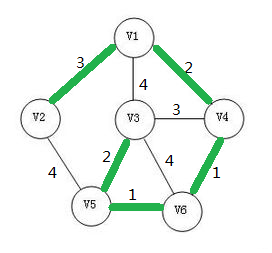
上图这个最小生成树的边权之和为9，是所有生成树中边权之和最小的。

---

Kruskal算法

（Kruskal算法适合稀疏图）

仍旧是那个无向连通图。。。

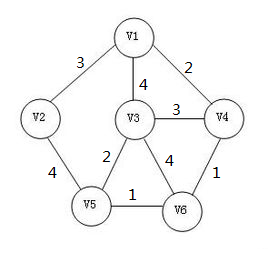
在这个图中有9个边。将这9条边按边权大小从小到大排序。紧接着将排好序的边挨个加入生成树中。没加入一条边便判断一下生成树是否有环。如果有，则将这条边移出生成树，换下一条边重新操作。

看不懂的看下面的示例：

首先选择边权最小的边加入生成树。（多个相等的边权则任意选择一个）

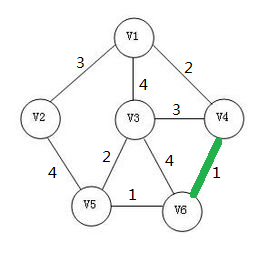
重复之前的操作。

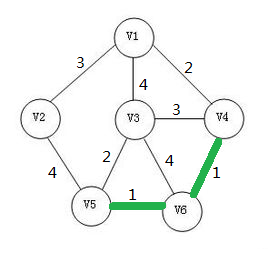
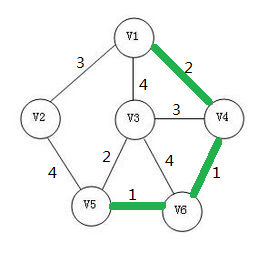
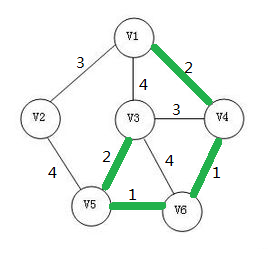
此时我再选择一条边加入生成树。

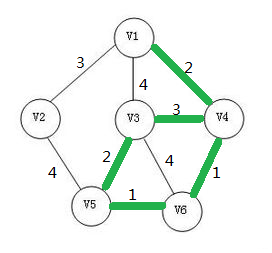
大家注意下图下面红色部分！！！

在加入一条边后生成树已经出现了一个环！！！

所以我们要退回之前。

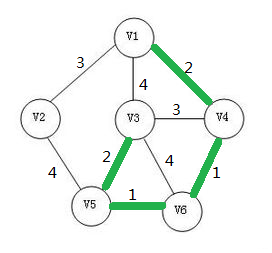
此时选择另外一条边。

此时并没有出现任何环。所以进行下一步。

我们发现这时的最小生成树刚好有n-1条边（一共n个点）。此时我们的最小生成树已经找完了。

---

Prim算法

（Prim算法适合稠密图）

那个无向连通图又来了。。。

（因为某些不可描述的原因，作者把图改了一下。。。）

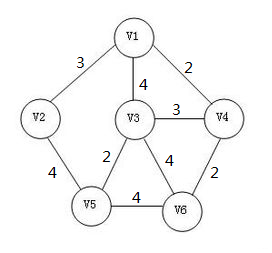
在此图中随便选择一个点加入生成树，然后选取所有可以取到的边（就是和生成树中的点连接的边）中边权最小的边加入生成树中，判断是否有环，然后重复此步骤。

看不懂的继续看例子啊

首先任意选取一个点。（例子选的是v1）

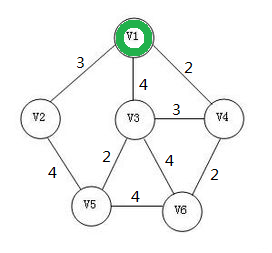
然后选取一个边权最小的边，并把点加入生成树。

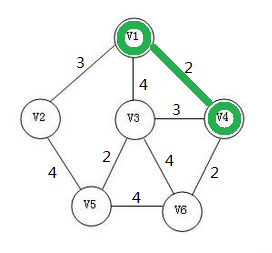
紧接着重复此步骤。

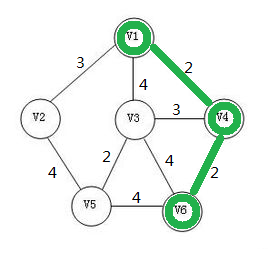
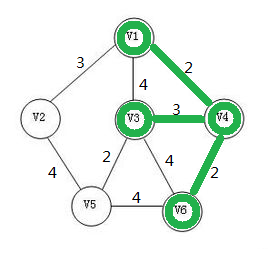
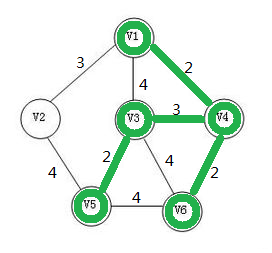
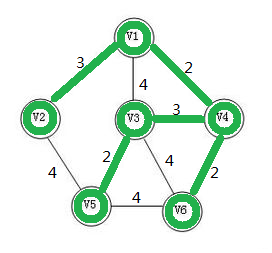
此时已经构成一棵最小生成树了。（PS：作者提示——作者没有做出现环的样例，请各位读者注意）

---

结束语：

本人第一篇博客。

有问题请指出，谢谢！