【数据结构】线段树（Segment Tree）

假设我们现在拿到了一个非常大的数组，对于这个数组里面的数字要反复不断地做两个操作。

1、（query）随机在这个数组中选一个区间，求出这个区间所有数的和。

2、（update）不断地随机修改这个数组中的某一个值。

时间复杂度：

枚举：

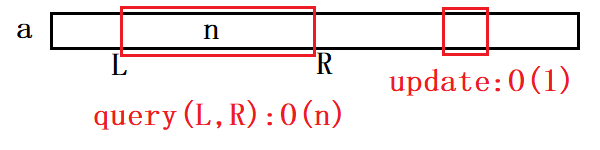
枚举L~R的每个数并累加。

• query：O（n）

找到要修改的数直接修改。

• update：O（1）

如果query与update要做很多很多次，query的O（n）会被卡住，所以时间复杂度会非常慢。那么有没有办法把query的时间复杂度降成O（1）呢？其中一种方法如下：

• 先建立一个与a数组一样大的数组。

• s[1]=a[1];s[2]=a[1]+a[2];s[3]=a[1]+a[2]+a[3];...;s[n]=a[1]+a[2]+a[3]+...+a[n]（在s数组中存入a的前缀和）

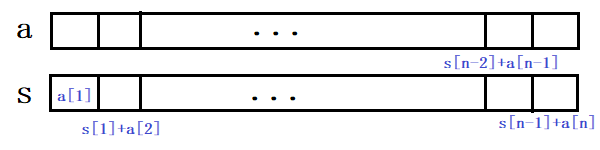
• 此时a[L]+a[L+1]+...+a[R]=s[R]-s[L-1]，query的时间复杂度降为O（1）。
• 但若要修改a[k]的值，随之也需修改s[k],s[k+1],...,s[n]的值，时间复杂度升为O（n）。

前缀和：

query：O（1）

update：O（n）

• 我们发现，当我们想尽方法把其中一个操作的时间复杂度改成O（1）后，另一个操作的时间复杂度就会变为O（n）。当query与update的操作特别多时，不论用哪种方法，总体的时间复杂度都不会特别快。
• 所以，我们将要讨论一种叫线段树的数据结构，它可以把这两个操作的时间复杂度平均一下，使得query和update的时间复杂度都落在O（n log n）上，从而增加整个算法的效率。

线段树

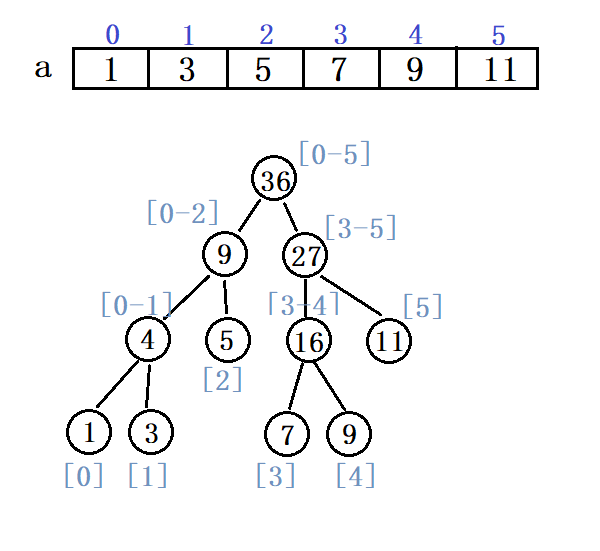
假设我们拿到了如下长度为6的数组：

在构建线段树之前，我们先阐述线段树的性质：

1、线段树的每个节点都代表一个区间。

2、线段树具有唯一的根节点，代表的区间是整个统计范围，如[1,N]。

3、线段树的每个叶节点都代表一个长度为1的元区间[x,x]。

4、对于每个内部节点[l,r]，它的左子结点是[l,mid]，右子节点是[mid+1,r]，其中mid=(l+r)/2（向下取整）。

依照这个数组，我们构建如下线段树（结点的性质为sum）：

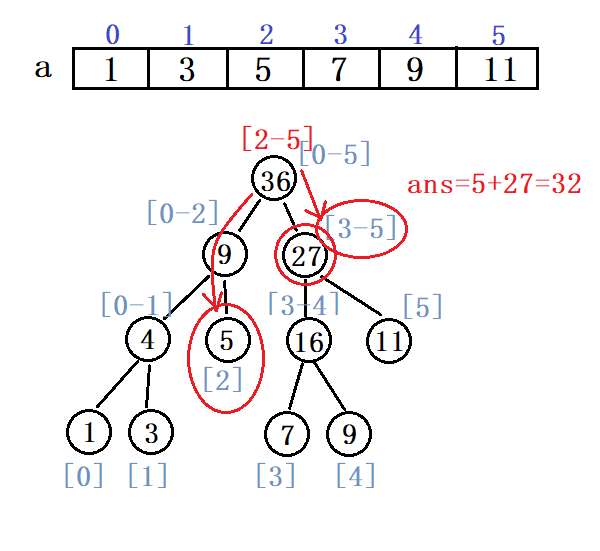
若我们要求[2-5]区间中数的和：

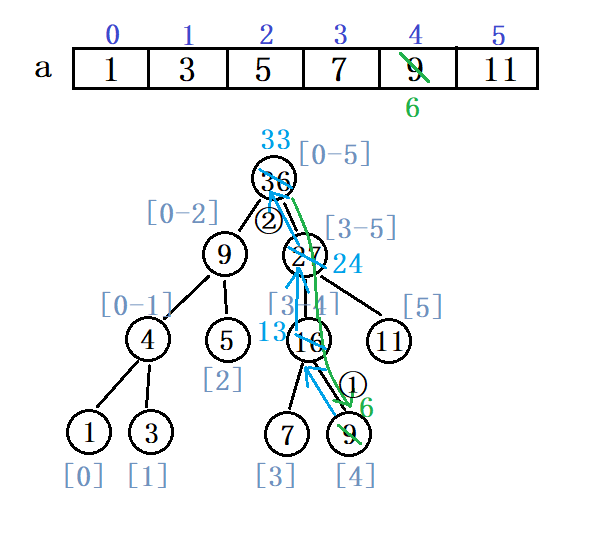
若我们要把a[4]改为6：

• 先一层一层找到目标节点修改，在依次向上修改当前节点的父节点。

接下来的问题是：如何保存这棵线段树？

• 用数组存储。

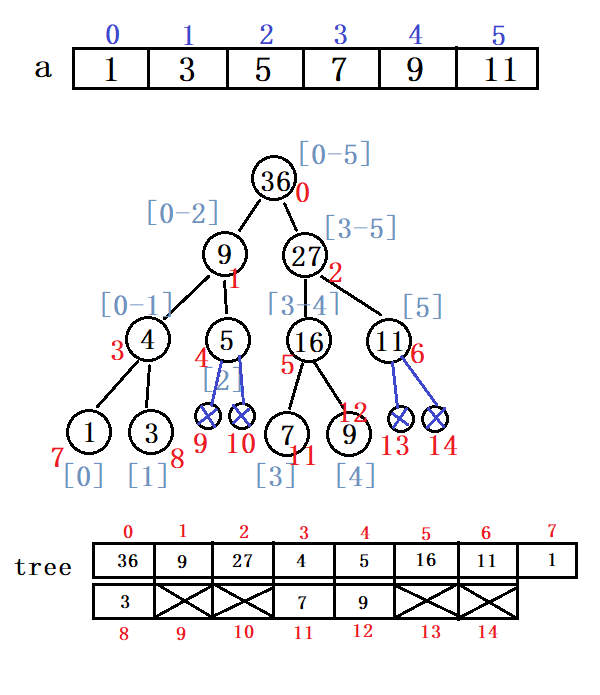
若我们要取node结点的左子结点（left）与右子节点（right），方法如下：

• left=2*node+1
• right=2*ndoe+2

举结点5为例（左子结点为节点11，右子节点为节点12）：

• left₅=2*5+1=11
• right₅=2*5+2=12

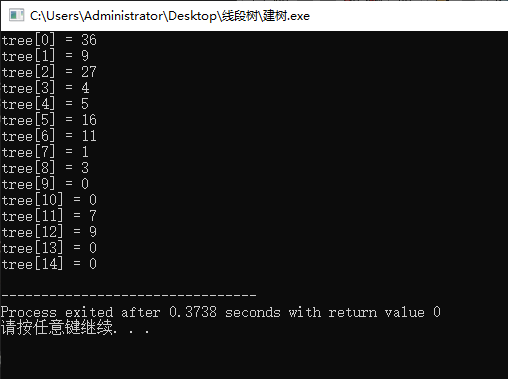
接下来给出建树的代码：

#include<bits/stdc++.h>
using namespace std; 

const int N = ;

int a[] = {, , , , , };
int size = ;
int tree[N] = {};

//建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
    //递归边界(即遇到叶子节点时)
    if (start == end){
        //直接存储a数组中的值
        tree[node] = a[start];
    } 

    else {
        //将建立的区间分成两半
        int mid = (start + end) / ;

        int left  =  * node + ;//左子节点的下标
        int right =  * node + ;//右子节点的下标 

        //求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
        build(a, tree, left,  start, mid);
        //求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
        build(a, tree, right, mid+, end);

        //当前节点的职位左子节点的值加上右子节点的值
        tree[node] = tree[left] + tree[right];
    }
}

int main(){
    //从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
    build(a, tree, , , size-);

    for(int i = ; i <= ; i ++)
        printf("tree[%d] = %d\n", i, tree[i]);

    return ;
}

运行结果：

update操作：

• 确定需要改的分支，向下寻找需要修改的节点，再向上修改节点值。
• 与建树的函数相比，update函数增加了两个参数x，val，即把a[x]改为val。

例：把a[x]改为6（代码实现）

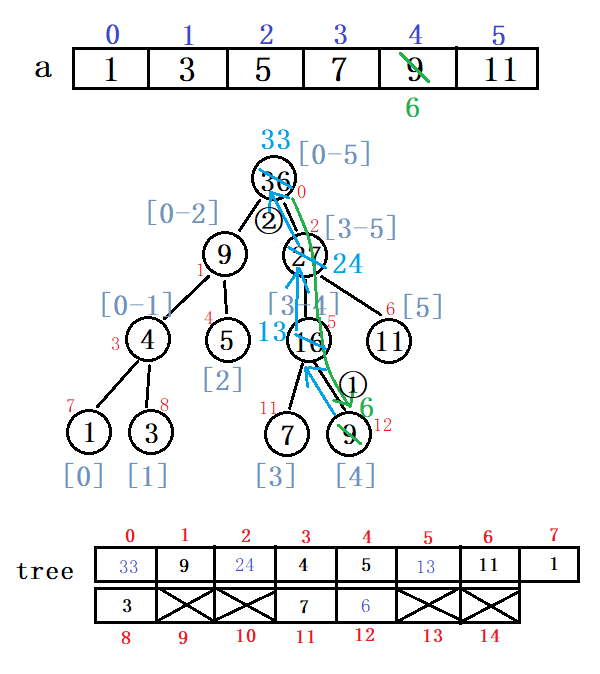
void update(int a[], int tree[], int node, int start, int end, int x, int val){
    //找到a[x],修改值
    if (start == end){
        a[x] = val;
        tree[node] = val;
    }

    else {
        int mid = (start + end) / ;

        int left  =  * node + ;
        int right =  * node + ;

        if (x >= start && x <= mid) {//如果x在左分支
            update(a, tree, start, mid, x, val);
        }
        else {//如果x在右分支
            update(a, tree, right, mid+, end, x, val);
        }

        //向上更新值
        tree[node] = tree[left] + tree[right];
    }
}

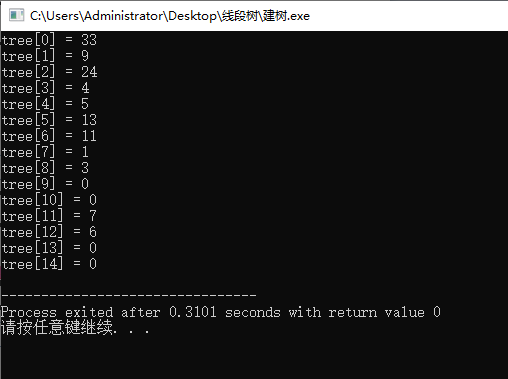
在主函数中调用：
//把a[x]改成6
update(a, tree, , , size-, , );

运行结果：

query操作：

• 向下依次寻找包含在目标区间中的区间，并累加。
• 与建树的函数相比，query函数增加了两个参数L，Rl，即把求a的区间[L,R]的和。

例：求a[2]+a[3]+...+a[5]的值（代码实现）

int query(int a[], int tree[], int node, int start, int end, int L,int R){
    //若目标区间与当时区间没有重叠,结束递归返回0
    if (start > R || end < L){
        return ;
    }

    //若目标区间包含当时区间,直接返回节点值
    else if (L <=start && end <= R){
        return tree[node];
    }

    else {
        int mid = (start + end) / ;

        int left  =  * node + ;
        int right =  * node + ;

        //计算左边区间的值
        int sum_left  = query(a, tree, left,  start, mid, L, R);
        //计算右边区间的值
        int sum_right = query(a, tree, right, mid+, end, L, R);

        //相加即为答案
        return sum_left + sum_right;
    }
}

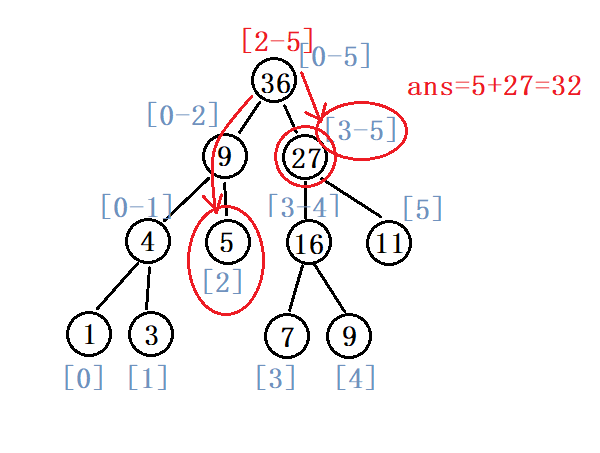
在主函数中调用：
//求区间[2,5]的和
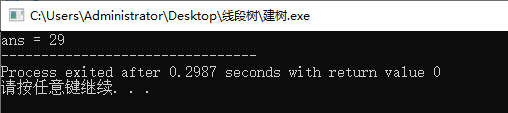
int ans = query(a, tree, , , size-, , );
printf("ans = %d", ans); 

运行结果：

最后，献上完整的代码：

#include<bits/stdc++.h>
using namespace std; 

const int N = ;

int a[] = {, , , , , };
int size = ;
int tree[N] = {};

//建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
    //递归边界(即遇到叶子节点时)
    if (start == end) {
        //直接存储a数组中的值
        tree[node] = a[start];
    } 

    else {
        //将建立的区间分成两半
        int mid = (start + end) / ;

        int left  =  * node + ;//左子节点的下标
        int right =  * node + ;//右子节点的下标 

        //求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
        build(a, tree, left,  start, mid);
        //求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
        build(a, tree, right, mid+, end);

        //当前节点的职位左子节点的值加上右子节点的值
        tree[node] = tree[left] + tree[right];
    }
}

void update(int a[], int tree[], int node, int start, int end, int x, int val){
    //找到a[x],修改值
    if (start == end){
        a[x] = val;
        tree[node] = val;
    }

    else {
        int mid = (start + end) / ;

        int left  =  * node + ;
        int right =  * node + ;

        if (x >= start && x <= mid) {//如果x在左分支
            update(a, tree, left, start, mid, x, val);
        }
        else {//如果x在右分支
            update(a, tree, right, mid+, end, x, val);
        }

        //向上更新值
        tree[node] = tree[left] + tree[right];
    }
}

//求a[L]~a[R]的区间和
int query(int a[], int tree[], int node, int start, int end, int L,int R){
    //若目标区间与当时区间没有重叠,结束递归返回0
    if (start > R || end < L){
        return ;
    }

    //若目标区间包含当时区间,直接返回节点值
    else if (L <=start && end <= R){
        return tree[node];
    }

    else {
        int mid = (start + end) / ;

        int left  =  * node + ;
        int right =  * node + ;

        //计算左边区间的值
        int sum_left  = query(a, tree, left,  start, mid, L, R);
        //计算右边区间的值
        int sum_right = query(a, tree, right, mid+, end, L, R);

        //相加即为答案
        return sum_left + sum_right;
    }
}

int main(){
    //从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
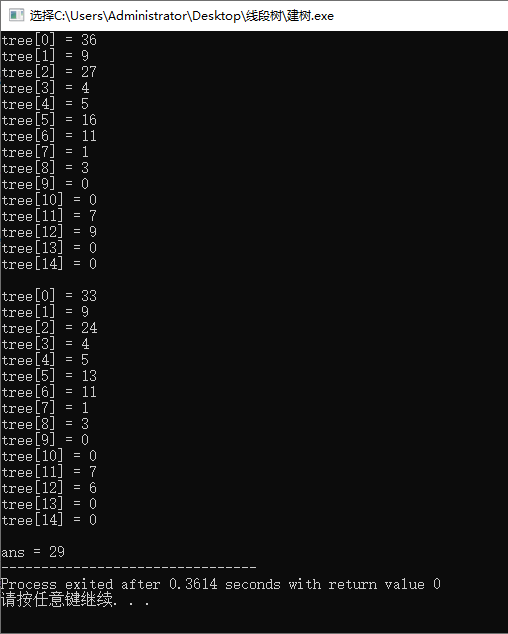
    build(a, tree, , , size-);

    for(int i = ; i <= ; i ++)
        printf("tree[%d] = %d\n", i, tree[i]);
    printf("\n");    

    //把a[x]改成6
    update(a, tree, , , size-, , ); 

    for(int i = ; i <= ; i ++)
        printf("tree[%d] = %d\n", i, tree[i]);
    printf("\n");

    //求区间[2,5]的和
    int ans = query(a, tree, , , size-, , );
    printf("ans = %d", ans); 

    return ;
}

运行结果：

学习视频链接