luogu P1084疫情控制 二分

链接

loj

luogu太水不要去了。

思路

二分。

每个军队在一定的时间内越往上越好。

注意一个军队可以跨过1去帮别的。

把能到1脚下的点都存下来特判。

有一种情况是这个子树内只有一个军队，但这个军队跑去帮别人了。

其他军队来帮这个子树。

就像这样。



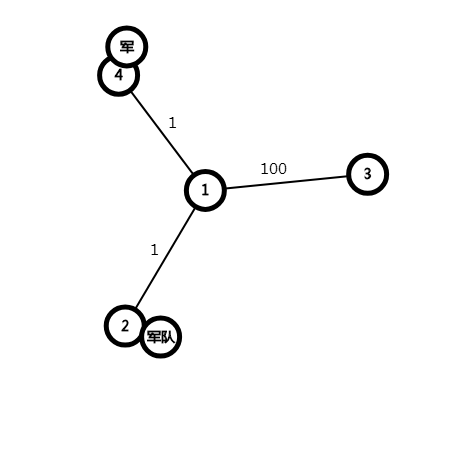
四号点的军队还有2秒钟，而且四号点有两个军队。

2号点有一个军队，还有101秒钟。

三号点没有军队。

四号点的一个军队到2，二号点的的军队到三。

这样的2号点放弃内部去外部的条件是什么？

答案是两倍的边权<剩余时间。

不然的话，四号店可以直接去拯救三号点了。

代码R的范围小了点，卡场过loj

代码

#include <iostream>
#include <vector>
#include <cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
using namespace std;
const int _=3e5+7;
const ll oo=0x3f3f3f3f3f3f3f;
char buf[10000001],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,10000000,stdin),p1==p2)?EOF:*p1++)
int read() {
	int x=0,f=1;char s=getchar();
	for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
	for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
	return x*f;
}
int n,m,pos[_],fa[_][19],vis[_],head[_],tot,ok[_];
ll sum[_],nb[_],cb[_];
struct node {int v,nxt,q;}e[_<<1];
void add(int u,int v,int q) {e[++tot].v=v,e[tot].q=q,e[tot].nxt=head[u],head[u]=tot;}
void init(int u,int f,ll tot) {
	fa[u][0]=f,sum[u]=tot;
	for(int i=head[u];i;i=e[i].nxt)
		if(e[i].v!=f) init(e[i].v,u,tot+e[i].q);
}
bool dfs(int u,int fa) {
	if(vis[u]) return 1;
	int siz=0;
	for(int i=head[u];i;i=e[i].nxt) {
		int v=e[i].v;
		if(v==fa) continue;
		siz++;
		if(!dfs(v,u)) return 0;
	} return siz;
}
vector<int> dsr[_];
bool cmp(int a,int b) {return sum[a]<sum[b];}
bool check(ll mid) {
	for(int i=1;i<=n;++i) vis[i]=ok[i]=0;
	for(int i=head[1];i;i=e[i].nxt) dsr[e[i].v].clear();
	for(int i=1;i<=m;++i) {
		int p=pos[i];
		for(int j=18;j>=0;--j)
			if(sum[pos[i]]-sum[fa[p][j]]<=mid)
				p=fa[p][j];
		if(fa[p][0]!=1) vis[p]++;
		else dsr[p].push_back(pos[i]);
	}
	for(int i=head[1];i;i=e[i].nxt) ok[e[i].v]=dfs(e[i].v,1);
	for(int i=head[1];i;i=e[i].nxt) sort(dsr[e[i].v].begin(),dsr[e[i].v].end(),cmp);
	for(int i=head[1];i;i=e[i].nxt) {
		int v=e[i].v;
		if(!ok[v] && dsr[v].size()) {
			ll x=mid-sum[dsr[v][dsr[v].size()-1]];
			if(e[i].q*2LL>=x) dsr[v].pop_back(),ok[v]=1;
		}
	}
	int cnt=0,gs=0;
	for(int i=head[1];i;i=e[i].nxt) {
		int v=e[i].v;
		for(int j=0;j<(int)dsr[v].size();++j)
			nb[++cnt]=mid-sum[dsr[v][j]];
		if(!ok[v]) cb[++gs]=e[i].q;
	}
	sort(nb+1,nb+1+cnt,greater<ll>());
	sort(cb+1,cb+1+gs,greater<ll>());
	if(cnt<gs) return 0;
	for(int i=1;i<=gs;++i) if(cb[i]>nb[i]) return 0;
	return 1;
}
int main() {
	n=read();
	for(int i=1;i<n;++i) {
		int u=read(),v=read(),w=read();
		add(u,v,w),add(v,u,w);
	}
	m=read();
	for(int i=1;i<=m;++i) pos[i]=read();
	init(1,0,0);
	sum[0]=sum[1]=-oo;
	for(int j=1;j<=18;++j)
		for(int i=1;i<=n;++i)
			fa[i][j]=fa[fa[i][j-1]][j-1];
	ll ans=1LL<<35LL;ans--;
	for(ll i=35;i>=0;--i)
		if(check(ans-(1LL<<i))) ans=ans^(1LL<<i);
	if(ans==((1LL<<35LL)-1)) ans=-1;
	cout<<ans<<"\n";
	return 0;
}