[LeetCode] 285. Inorder Successor in BST 二叉搜索树中的中序后继节点

Given a binary search tree and a node in it, find the in-order successor of that node in the BST.

The successor of a node p is the node with the smallest key greater than p.val.

Example 1:

Input: root = [2,1,3], p = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both p and the return value is of TreeNode type.

Example 2:

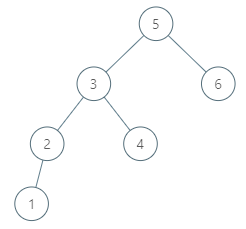
Input: root = [5,3,6,2,4,null,null,1], p = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Note:

1. If the given node has no in-order successor in the tree, return null.
2. It's guaranteed that the values of the tree are unique.

这道题让我们求二叉搜索树的某个节点的中序后继节点，那么根据 BST 的性质知道其中序遍历的结果是有序的，博主最先用的方法是用迭代的中序遍历方法，然后用一个 bool 型的变量b，初始化为 false，进行中序遍历，对于遍历到的节点，首先看如果此时b已经为 true，说明之前遍历到了p，那么此时返回当前节点，如果b仍为 false，看遍历到的节点和p是否相同，如果相同，此时将b赋为 true，那么下一个遍历到的节点就能返回了，参见代码如下：

解法一：

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        stack<TreeNode*> s;
        bool b = false;
        TreeNode *t = root;
        while (t || !s.empty()) {
            while (t) {
                s.push(t);
                t = t->left;
            }
            t = s.top(); s.pop();
            if (b) return t;
            if (t == p) b = true;
            t = t->right;
        }
        return NULL;
    }
};

下面这种方法是用的中序遍历的递归写法，需要两个全局变量 pre 和 suc，分别用来记录祖先节点和后继节点，初始化将他们都赋为 NULL，然后在进行递归中序遍历时，对于遍历到的节点，首先看 pre 和p是否相同，如果相同，则 suc 赋为当前节点，然后将 pre 赋为 root，那么在遍历下一个节点时，pre 就起到记录上一个节点的作用，参见代码如下：

解法二：

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if (!p) return NULL;
        inorder(root, p);
        return suc;
    }
    void inorder(TreeNode *root, TreeNode *p) {
        if (!root) return;
        inorder(root->left, p);
        if (pre == p) suc = root;
        pre = root;
        inorder(root->right, p);
    }
private:
    TreeNode *pre = NULL, *suc = NULL;
};

再来看一种更简单的方法，这种方法充分地利用到了 BST 的性质，首先看根节点值和p节点值的大小，如果根节点值大，说明p节点肯定在左子树中，那么此时先将 res 赋为 root，然后 root 移到其左子节点，循环的条件是 root 存在，再比较此时 root 值和p节点值的大小，如果还是 root 值大，重复上面的操作，如果p节点值，那么将 root 移到其右子节点，这样当 root 为空时，res 指向的就是p的后继节点，参见代码如下：

解法三：

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode *res = NULL;
        while (root) {
            if (root->val > p->val) {
                res = root;
                root = root->left;
            } else root = root->right;
        }
        return res;
    }
};

上面那种方法也可以写成递归形式，写法也比较简洁，但是需要把思路理清，当根节点值小于等于p节点值，说明p的后继节点一定在右子树中，所以对右子节点递归调用此函数，如果根节点值大于p节点值，那么有可能根节点就是p的后继节点，或者左子树中的某个节点是p的后继节点，所以先对左子节点递归调用此函数，如果返回空，说明根节点是后继节点，返回即可，如果不为空，则将那个节点返回，参见代码如下：

解法四:

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if (!root) return NULL;
        if (root->val <= p->val) {
            return inorderSuccessor(root->right, p);
        } else {
            TreeNode *left = inorderSuccessor(root->left, p);
            return left ? left : root;
        }
    }
};

Github 同步地址：

https://github.com/grandyang/leetcode/issues/285

类似题目：

Binary Search Tree Iterator

Binary Tree Inorder Traversal

Inorder Successor in BST II

参考资料：

https://leetcode.com/problems/inorder-successor-in-bst/

https://leetcode.com/problems/inorder-successor-in-bst/discuss/72653/Share-my-Java-recursive-solution

https://leetcode.com/problems/inorder-successor-in-bst/discuss/72662/*Java*-5ms-short-code-with-explanations

https://leetcode.com/problems/inorder-successor-in-bst/discuss/72656/JavaPython-solution-O(h)-time-and-O(1)-space-iterative

LeetCode All in One 题目讲解汇总(持续更新中...)