BZOJ 2005: [Noi2010]能量采集(莫比乌斯反演)
http://www.lydsy.com/JudgeOnline/problem.php?id=2005
题意:

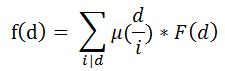

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<sstream>
#include<vector>
#include<stack>
#include<queue>
#include<cmath>
#include<map>
#include<set>
using namespace std;
typedef long long ll;
typedef pair<int,int> pll;
const int INF = 0x3f3f3f3f;
const int maxn = + ; bool check[maxn];
int prime[maxn];
int mu[maxn];
ll sum[maxn]; void Mobius()
{
memset(check, false, sizeof(check));
mu[] = ;
int tot = ;
for (int i = ; i <= maxn; i++)
{
if (!check[i])
{
prime[tot++] = i;
mu[i] = -;
}
for (int j = ; j < tot; j++)
{
if (i * prime[j] > maxn)
{
break;
}
check[i * prime[j]] = true;
if (i % prime[j] == )
{
mu[i * prime[j]] = ;
break;
}
else
{
mu[i * prime[j]] = -mu[i];
}
}
}
sum[]=;
for(int i=;i<maxn;i++)
sum[i]=sum[i-]+mu[i];
return ;
} ll solve(int n, int m)
{
if(n>m) swap(n,m);
ll tmp=;
for(int i=,last=;i<=n;i=last+)
{
last=min(n/(n/i),m/(m/i));
tmp+=(sum[last]-sum[i-])*(n/i)*(m/i);
}
return tmp;
} int n, m; int main()
{
//freopen("in.txt","r",stdin);
Mobius();
while(~scanf("%d%d",&m,&n))
{
ll ans=;
for(int i=;i<=min(n,m);i++) //枚举d
ans+=solve(n/i,m/i)*i; //这儿求gcd(x,y)=d的对数,但是如果/i的话就相当于计算gcd(x,y)=1的对数
//简化了计算
printf("%lld\n",*ans-(ll)n*m);
}
return ;
}
BZOJ 2005: [Noi2010]能量采集(莫比乌斯反演)的更多相关文章
- BZOJ 2005: [Noi2010]能量采集 [莫比乌斯反演]
题意:\((0,0)\)到\((x,y),\ x \le n, y \le m\)连线上的整点数\(*2-1\)的和 \((0,0)\)到\((a,b)\)的整点数就是\(gcd(a,b)\) 因为. ...
- BZOJ 2005 [Noi2010]能量采集 (数学+容斥 或 莫比乌斯反演)
2005: [Noi2010]能量采集 Time Limit: 10 Sec Memory Limit: 552 MBSubmit: 4493 Solved: 2695[Submit][Statu ...
- bzoj 2005: [Noi2010]能量采集 筛法||欧拉||莫比乌斯
2005: [Noi2010]能量采集 Time Limit: 10 Sec Memory Limit: 552 MB[Submit][Status][Discuss] Description 栋栋 ...
- BZOJ 2005: [Noi2010]能量采集
2005: [Noi2010]能量采集 Time Limit: 10 Sec Memory Limit: 552 MBSubmit: 3312 Solved: 1971[Submit][Statu ...
- BZOJ 2005: [Noi2010]能量采集( 数论 + 容斥原理 )
一个点(x, y)的能量损失为 (gcd(x, y) - 1) * 2 + 1 = gcd(x, y) * 2 - 1. 设g(i)为 gcd(x, y) = i ( 1 <= x <= ...
- luogu1447 [NOI2010]能量采集 莫比乌斯反演
link 冬令营考炸了,我这个菜鸡只好颓废数学题了 NOI2010能量采集 由题意可以写出式子: \(\sum_{i=1}^n\sum_{j=1}^m(2\gcd(i,j)-1)\) \(=2\sum ...
- bzoj 2005: [Noi2010]能量采集【莫比乌斯反演】
注意到k=gcd(x,y)-1,所以答案是 \[ 2*(\sum_{i=1}^{n}\sum_{i=1}^{m}gcd(i,j))-n*m \] 去掉前面的乘和后面的减,用莫比乌斯反演来推,设n< ...
- BZOJ2005: [Noi2010]能量采集 莫比乌斯反演的另一种方法——nlogn筛
分析:http://www.cnblogs.com/huhuuu/archive/2011/11/25/2263803.html 注:从这个题收获了两点 1,第一象限(x,y)到(0,0)的线段上整点 ...
- 【刷题】BZOJ 2005 [Noi2010]能量采集
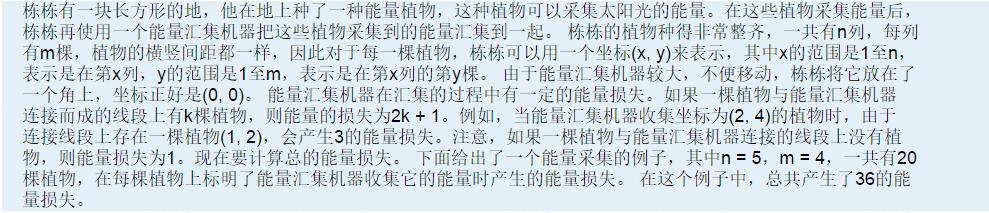
Description 栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量.在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起. 栋栋的植物种得 ...
- BZOJ2005:[NOI2010]能量采集(莫比乌斯反演,欧拉函数)
Description 栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量.在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起. 栋栋的植物种得 ...
随机推荐
- Unity3D 笔记一 初始Unity3D
一.初步认识Unity 1.Unity支持C#.JavaScript.Boo,JavaScript不是标准语法,常称为UnityScript更合适 2.Update 每一帧都会调用该方法.Start. ...
- 音频的录制和播放功能(audio) ---- HTML5+
模块:audio Audio模块用于提供音频的录制和播放功能,可调用系统的麦克风设备进行录音操作,也可调用系统的扬声器设备播放音频文件.通过plus.audio获取音频管理对象. 应用场景:音频录制, ...
- 问答项目---金币经验奖励规则及网站配置写入config文件
具体步骤: 引入配置文件——>获取当前数组——>进行合并 public function edit(){ //引入 config.php配置文件 $file = APP_PATH.'Com ...
- 混合开发中ios兼容问题
1. z-index无效,设置层级,发现再ios中无效,后来发现是设置了 -webkit-overflow-scrolling:touch 设置这个属性之后.层级设置失效 2.@keyup事件的问题, ...
- postgresql----UNION&&INTERSECT&&EXCEPT
多个SELECT语句可以使用UNION,INTERSECT和EXCEPT进行集合处理,其中UNION用于求并集,INTERSECT用于求交集,EXCEPT用于求差集.用法如下 query1 UNION ...
- javascript飞机大战-----007爆炸效果
要检验什么时候碰撞,我们必须了解什么时候不相撞.以上四种情况是不相撞的时候 首先在引擎里面写好什么时候碰撞什么时候不碰撞 /* 游戏引擎 */ var Engine = { //刚开始的游戏状态 ga ...
- yii2.0 如何按需加载并管理CSS样式及JS脚本
链接:http://www.yiichina.com/tutorial/399 (注:以下为Yii2.0高级应用测试) Yii2.0对于CSS/JS 管理,使用AssetBundle资源包类. 视图如 ...
- Java中实现序列化的两种方式 Serializable 接口和 Externalizable接口
对象的序列化就是将对象写入输出流中. 反序列化就是从输入流中将对象读取出来. 用来实现序列化的类都在java.io包中,我们常用的类或接口有: ObjectOutputStream:提供序列化对象并把 ...
- Oracle管理监控之段空间利用监控-oracle性能优化
SELECT S.OWNER, S.SEGMENT_NAME, S.SEGMENT_TYPE, S.PARTITION_NAME, ROUND(BYTE ...
- MyBatis 内置日志工厂基于运行时自省机制选择合适的日志工具
mybatis – MyBatis 3 | 日志 http://www.mybatis.org/mybatis-3/zh/logging.html MyBatis 内置日志工厂基于运行时自省机制选择合 ...
