WHU 1540 Fibonacci 递推

武大邀请赛的网络预选赛，就去做了个签到题，居然连这个递推都没推出来，真是惭愧。

而且好久没写矩阵乘法了，来回顾一下。

题意：

　　求Fibonacci数列的，前n项立方和。

思路：

　　可以求得一下递推公式：

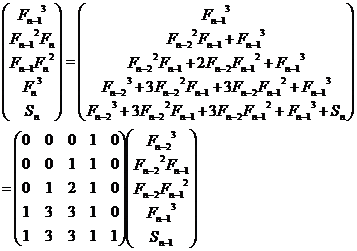
然后用矩阵快速幂求出结果即可。

代码：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <functional>

 using namespace std;

 typedef long long ll;

 const ll MOD  = (ll)1e9+;
 const ll ONE[][] = {
     {, , , , },
     {, , , , },
     {, , , , },
     {, , , , },
     {, , , , },
 };
 const ll MU[][] = {
     {, , , , },
     {, , , , },
     {, , , , },
     {, , , , },
     {, , , , },
 };
 const ll v1[] = {, , , , };
 struct Matrix {
     ll body[][];

     Matrix() {}
     Matrix(bool x) {
         if (x) {
             for (int i = ; i < ; i++)
                 for (int j = ; j < ; j++)
                     body[i][j] = ONE[i][j];
         } else {
             for (int i = ; i < ; i++)
                 for (int j = ; j < ; j++)
                     body[i][j] = MU[i][j];
         }
     }

     Matrix operator * (const Matrix &x) {
         Matrix res;
         ll tmp = ;
         for (int i = ; i < ; i++)
             for (int j = ; j < ; j++) {
                 tmp = ;
                 for (int k = ; k < ; k++)
                     tmp = (tmp+(body[i][k]*x.body[k][j])%MOD)%MOD;
                 res.body[i][j] = tmp;
             }
         return res;
     }
 };

 Matrix pow(int k){
     Matrix res(true);
     Matrix d(false);
     while (k>) {
         if (k&) res = res*d;
         d = d*d;
         k >>= ;
     }
     return res;
 }

 int n;
 ll v2[];

 int main() {
     #ifdef Phantom01
         freopen("WHU1540.txt", "r", stdin);
     #endif // Phantom01

     while (scanf("%d", &n)!=EOF) {
         if (==n) break;

         if (n<=) {
             printf("%d\n", n);
             continue;
         }
         Matrix tmp = pow(n-);
         ll t = ;
         for (int i = ; i < ; i++) {
             t = ;
             for (int j = ; j < ; j++)
                 t = (t+(tmp.body[i][j]*v1[j])%MOD)%MOD;
             v2[i] = t;
         }
         printf("%d\n", (int)v2[]);
     }

     return ;
 }