0x03 递归

这个东西好像在搞矩乘的时候用过？忘了

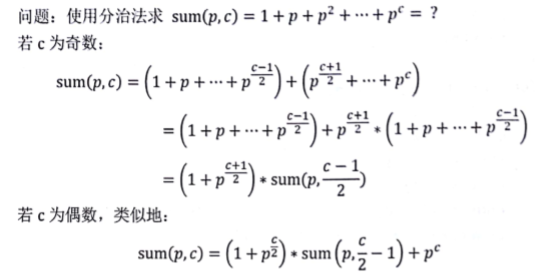
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL;
const int mod=;

int len;LL zy[],cs[];
void get_zy(LL n)
{
    len=;
    for(LL i=;i*i<=n;i++)
    {
        if(n%i==)
        {
            len++;
            zy[len]=i;cs[len]=;
            while(n%i==)n/=i,cs[len]++;
        }
    }
    if(n>) len++, zy[len]=n, cs[len]=;
}

//---------------------------------

LL quick_power(LL n,int p)
{
    LL A=n%mod,ret=;
    while(p>)
    {
        if(p%==)ret=(ret*A)%mod;
        A=(A*A)%mod;p/=;
    }
    return ret;
}
LL fenzi(LL n,int p)
{
    if(p==)return ;
    if(p%==)
    {
        return (( fenzi(n,p/-)*(+quick_power(n,p/)) )%mod+quick_power(n,p))%mod;
    }
    else
    {
        return ( fenzi(n,p/)*(+quick_power(n,p/+)) )%mod;
    }
}
int main()
{
    LL n;int p;
    while(scanf("%lld%d",&n,&p)!=EOF)
    {
        get_zy(n);

        LL ans=;
        for(int i=;i<=len;i++)
        {
            ans=(ans*fenzi(zy[i],cs[i]*p))%mod;
        }
        printf("%lld\n",ans);
    }
    return ;
}

poj1845

3889那题太无聊了，题意还贼难理解，YY了下做法，就是很裸分治找在那个位置，维护横纵区间

手工栈太麻烦了，看这题吧bzoj2819Nim 但是好像机友们只传1个参数的搜索也可以

总的来讲没什么意思。

upd：

填坑：poj3889一道分形题，这种通过搜索变量交换进行翻转的题挺好的。反正自己肯定看得懂就不详写了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long LL; 

LL Bin[];
void dfs(LL n,LL k,LL &x,LL &y)
{
    if(n==)
    {
        if(k==)x=,y=;
        else if(k==)x=,y=;
        else if(k==)x=,y=;
        else x=,y=;
        return ;
    }

    LL d=Bin[n-]*Bin[n-];
    if(k<=d)//左上
    {
        dfs(n-,k,y,x);
    }
    else if(k<=*d)//右上
    {
        dfs(n-,k-d,x,y);
        y+=Bin[n-];
    }
    else if(k<=*d)//右下
    {
        dfs(n-,k-*d,x,y);
        x+=Bin[n-];y+=Bin[n-];
    }
    else//左下
    {
        dfs(n-,k-*d,y,x);
        x=Bin[n]+-x;y=Bin[n-]+-y;
    }
}

int main()
{
    Bin[]=;for(int i=;i<=;i++)Bin[i]=Bin[i-]*2LL;
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n,st,ed;
        scanf("%lld%lld%lld",&n,&st,&ed);
        LL stx,sty,edx,edy;
        dfs(n,st,stx,sty),dfs(n,ed,edx,edy);
        printf("%.0lf\n",sqrt(double((stx-edx)*(stx-edx)+(sty-edy)*(sty-edy)))*);
    }
    return ;
}

poj3889