并查集（disjoint set）的实现及应用

这里有一篇十分精彩、生动的 并查集详解 (转)；

• “朋友的朋友就是朋友”⇒ 传递性，建立连通关系

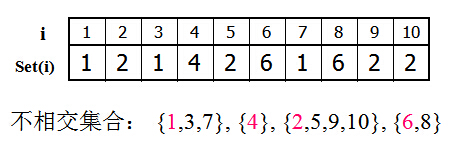
disjoint set，并查集（一种集合），也叫不相交集，同时也是一种树型的数据结构；用于处理一些不相交集合（Disjoint Sets）的合并（merge）及查询（find）问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合，也就是按一定顺序将属于同一组的元素所在的集合合并。

并查集的构成：

• 整数型的数组

  • 数组 pre[] 记录了每个点的前导点是什么，pred[] ⇒ 会形成一棵树形结构，树形结构的根，即为整棵树的代表（reps）

  

• 两个函数构成

  • 函数 find 是查找；
  • join 是合并；

1. 简单实现

• find（暂不考虑，路径压缩的问题，path compression）

  int pred[1000];
  
  int find(int x){
      int r = x;
      while (r != pred[r]){
          r = pred[r];
      }
      return r;
  }

• join

  void find(int x, int y){
      int rx = find(x), ry = find(y);
      if (rx != ry)
          pred[rx] = ry;
                              // 因为 rx 是 x 等的代表 ⇒ pred[rx] == rx
                              // 如此以来，x 所在的树，y 所在的树就实现了连通；
  }

2. 含有路径压缩的实现

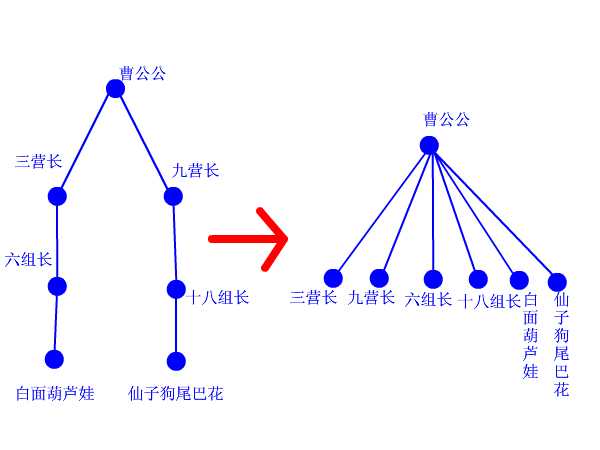
路径压缩的概念可通过下图清晰地展示出来，

路径压缩之后，减少了中间的传递过程，一步直达根节点（总代表）；

但需要注意的是，执行一次 find，只把一个分支，统一化为两层结构；

int find(int x)
{
    int r=x;
    while(r!=pre[r])
        r=pre[r];  

    int i=x,j;
    while(pre[i]!=r)
    {
        j=pre[i];
        pre[i]=r;
        i=j;
    }
    return r;
}