国庆 day 3 下午

a
【问题描述】
　　　　　　你是能看到第一题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　——hja
　　　　给你一个只有小括号和中括号和大括号的括号序列，问该序列是否合法。
【输入格式】
　　一行一个括号序列。
【输出格式】
　　如果合法，输出 OK，否则输出 Wrong。
【样例输入】
　　[(])
【样例输出】
　　Wrong
【数据范围与规定】
　　对于70%的数据，1 ≤n≤ 100。
　　对于100%的数据，1 ≤ n≤ 10000，所有单词由大写字母组成。
P100 zhxb
思路：栈维护一下。

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
string s;
char stack[];
int top,m1,m2,m3;
int main(){
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    cin>>s;
    int len=s.length();
    for(int i=;i<len;i++){
        if(s[i]=='(') {m1++;stack[top++]=s[i];}
        if(s[i]=='[') {m2++;stack[top++]=s[i];}
        if(s[i]=='{') {m3++;stack[top++]=s[i];}
        else if(s[i]==')'){
            if(!m1){cout<<"Wrong";return ;}
            else if(stack[top-]!='('){cout<<"Wrong";return ;}
            else{top--;m1--;}
        }
        else if(s[i]==']'){
            if(!m2){cout<<"Wrong";return ;}
            else if(stack[top-]!='['){cout<<"Wrong";return ;}
            else {top--;m2--;}
        }
        else if(s[i]=='}'){
            if(!m3){cout<<"Wrong";return ;}
            else if(stack[top-]!='{'){cout<<"Wrong";return ;}
            else {top--;m3--;}
        }
    }
    if(top||m1||m2||m3) cout<<"Wrong";
    else cout<<"OK";
}

b
【问题描述】
　　　　　　你是能看到第二题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　——laekov
　　　　Yjq 想要将一个长为l宽为w的矩形棺材（棺材表面绝对光滑，所以棺材可
　　以任意的滑动）拖过一个 L 型墓道。
　　　　如图所示，L 型墓道两个走廊的宽度分别是a和b，呈 90°，并且走廊的长
　　度远大于?。
　　　　现在 Hja 想知道对于给定的a,b,l，最大的?是多少，如果无论如何棺材都
　　不可能通过，则输出"My poor head =("
【输入格式】
　　第一行三个用空格分隔的整数a,b,l，意义如题目所示。
【输出格式】
　　输出最大的可能的?，保留七位小数，如果无论如何棺材都不可能通过，则
　　输出"My poor head =("。
【样例输入 1】
　　2 2 1
【样例输出 1】
　　1.0000000

【样例输入 2】
　　2 2 2
【样例输出 2】
　　2.0000000
【样例输入 3】
　　2 2 3
【样例输出 3】
　　1.3284271
【样例输入 4】
　　2 2 6
【样例输出 4】
　　My poor head =(
【数据范围与规定】
　　对于100%的数据，1 ≤ a,b,l ≤ 10 ⁴ 。
　　P100 zhxc

以下解题思路来自xxy大佬的博客。

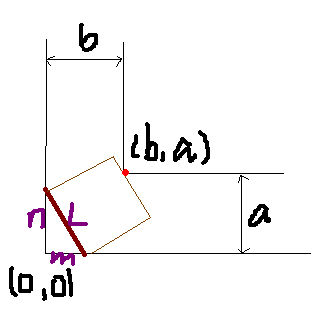
设直线解析式为 y=（-n/m）* x+n

整理，得：- n * x + m * y + n * m = 0

点（b，a）到直线的距离为：| - b * n - a * m + n * m | / L

(L : 根号下（n^2 + m^2）=L)

最优解就是 - b * n - a * m + n * m 的最大值

然后不知道为啥求了个

b * n + a * m - n *m 的最小值

单峰函数求最小值，三分法每次去掉大的一部分

式子最小值<0 时无解

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const double eps=1e-;
int a,b,l;
double L=,R=;
double ans=0x7f7f7f7f;
double mid1,mid2,t1,t2;
double f(double n){
    double m=sqrt(1.0*l*l-n-n);
    if(n*m>a*n+b*m)    return -;
    return (b*m+a*n-n*m)/l;
}
int main(){
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    scanf("%d%d%d",&a,&b,&l);
    if(a>=&&b>=){
        printf("%d.0000000",l);
        return ;
    }
    if(a>=l){
        printf("%d.0000000",b);
        return ;
    }
    if(b>=){
        printf("%d.0000000",a);
        return ;
    }
    int t=;
    while(t--){
        mid1=(R-L)/+L;
        mid2=L+R-mid1;
        t1=f(mid1);
        t2=f(mid2);
        if(t1<||t2<){
            printf("My poor head =(");
            return ;
        }
        if(t1<t2){
            ans=min(ans,t1);
            R=mid2;
        }
        else{
            ans=min(ans,t2);
            L=mid1;
        }
    }
    printf("%.7lf",ans);
}

c
【问题描述】
　　　　　　你是能看到第三题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　——aoao
　　　　树是个好东西，删掉树一条边要 1 的代价，随便再加一条边有 1 的代价，求
　　最小的代价把树变成环。
【输入格式】
　　第一行一个整数n，代表树的点数。
　　接下来n − 1行，每行两个数代表树的一条边。
【输出格式】
　　一行一个整数代表答案。
【样例输入】
　　4
　　1 2
　　2 3
　　2 4
【样例输出】
　　3
【数据规模与约定】
　　对于30%的数据，1≤n≤10。
　　对于60%的数据，1 ≤ n ≤ 1000。
　　对于100%的数据，1 ≤ n ≤ 100000。

思路：贪心。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100010
using namespace std;
int n,tot,ans,root;
int into[MAXN];
int to[MAXN*],net[MAXN*],head[MAXN*];
void add(int u,int v){
    to[++tot]=v;net[tot]=head[u];head[u]=tot;
    to[++tot]=u;net[tot]=head[v];head[v]=tot;
}
void dfs(int now,int fa){
    for(int i=head[now];i;i=net[i])
        if(to[i]!=fa){
            dfs(to[i],now);
            if(into[to[i]]>){
                into[now]--;
                ans+=(into[to[i]]-)*;
            }
        }
}
int main(){
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    scanf("%d",&n);
    for(int i=;i<n;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
        into[u]++;
        into[v]++;
    }
    root=;
    for(int i=;i<=n;i++)
        if(into[i]==){
            root=i;
            break;
        }
    dfs(root,-);
    cout<<ans+;
}
/*
8
1 2
1 3
3 4
3 5
4 6
4 7
4 8
3
*/