湖南集训day4

难度:☆☆☆☆☆☆☆

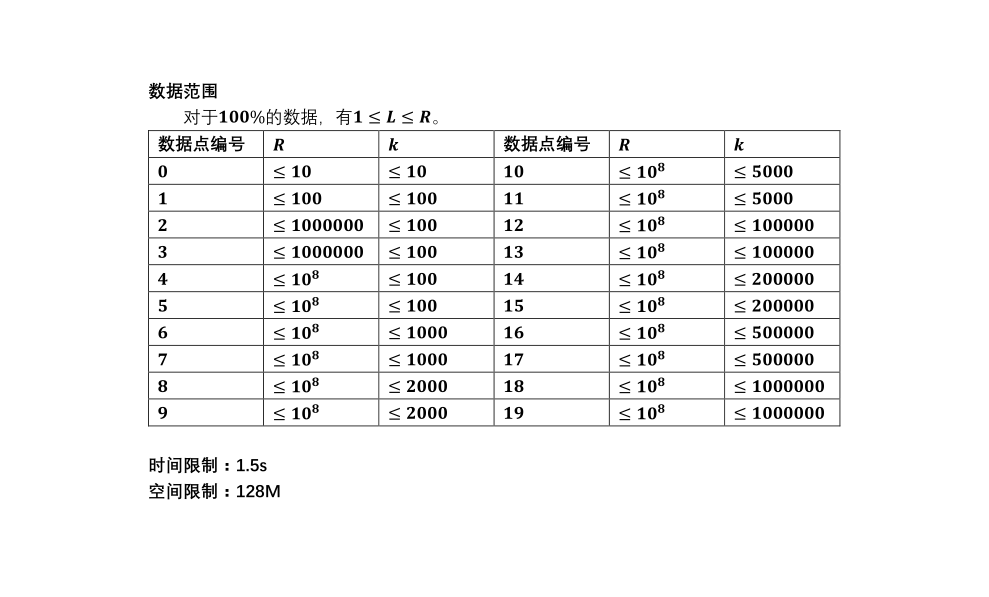
题解: 有个定理，另sum(x)表示小于等于x的数中与x互质的数的和

sum(x)=φ(x)*x/2    最后可知f(x)=x  （f(1)=2）  当然打表能知道。

然后就转化为了求Σi^k

然后就是拉格朗日插值法了，不在我理解范畴........

但这个博客介绍挺好哒 http://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html

std：

#include <cstring>
#include <ctime>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>

using namespace std;

const int Mod=998244353;
const int MAXK=1000000;

int power(int x,int k)
{
	int ret=1;
	while (k)
	{
		if (k&1) ret=1LL*ret*x%Mod;
		x=1LL*x*x%Mod;
		k>>=1;
	}
	return ret;
}

int k;

int f[MAXK+10];

int pre[MAXK+10],suf[MAXK+10];

int jc[MAXK+10],K[MAXK+10];

int cnt(int n)
{
	if (n==0) return 0;
	int ans=0;
	if (n<=k+10 || n<=MAXK)
	{
		for (int i=1; i<=n; i++) ans=(K[i]+ans)%Mod;
	}
	else
	{
		pre[0]=1;
		for (int i=1; i<=k+2; i++) pre[i]=1LL*pre[i-1]*(n-i)%Mod;

		suf[k+3]=1;
		for (int i=k+2; i>=1; i--) suf[i]=1LL*suf[i+1]*(n-i)%Mod;

		int l=k+1,r=0,flag=((k+1)&1)?(-1):(1);
		for (int i=1; i<=k+2; i++)
		{
			int s=1LL*pre[i-1]*suf[i+1]%Mod,m=1LL*(flag*jc[l]+Mod)*jc[r]%Mod;
			ans=(1LL*f[i]*s%Mod*power(m,Mod-2)%Mod+ans)%Mod;
			l--;
			r++;
			flag*=-1;
		}
	}
	ans=((ans+K[2])%Mod-1+Mod)%Mod;
	return ans;
}

int L,R;

void init()
{
	cin>>L>>R>>k;
	for (int i=1; i<=MAXK+5; i++) K[i]=power(i,k);

	jc[0]=1;
	for (int i=1; i<=k+2; i++) jc[i]=1LL*jc[i-1]*i%Mod;
	for (int i=1; i<=k+2; i++) f[i]=(f[i-1]+K[i])%Mod;

	cout<<(cnt(R)-cnt(L-1)+Mod)%Mod;
	return ;
}

int main()
{
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	init();
	fclose(stdin);
	fclose(stdout);
	//fprintf(stderr,"%.3lf\n",1.0*clock()/(1.0*CLOCKS_PER_SEC));
	return 0;
}

　　

/*
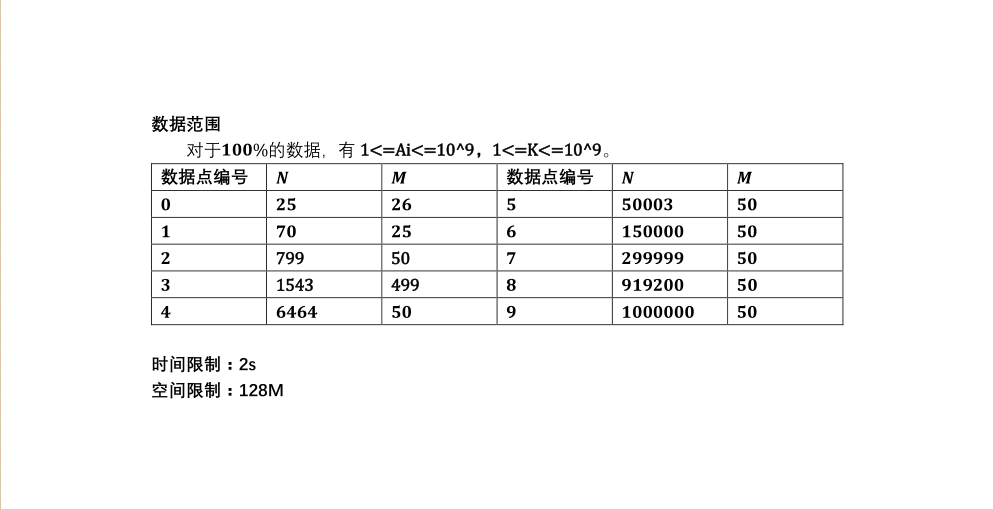
题意转化为求最大的区间长度使得这段区间和减k>=0
首先做前缀和，可知若当前到了k,i<j<k && sum[i]<sum[j]则j一定不可能比i更优
用单调栈维护这个过程。然后倒序更新答案即可。
*/ 

#include<iostream>
#include<cstdio>
#include<cstring>

#define N 1000007

using namespace std;
long long sum[N];
int a[N],st[N],top,n,m,cnt;

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

void solve(int k)
{
    top=;int res=;
    for(int i=;i<=n;i++)
    {
        sum[i]=sum[i-]+a[i]-k;
        if(!top || sum[st[top]]>sum[i]) st[++top]=i;
    }
    for(int i=n;i>=;i--)
    {
        while(top && sum[i]>=sum[st[top]]) top--;
        res=max(res,i-st[top+]);
    }
    printf("%d ",res);
}

int main()
{
    freopen("blocks.in","r",stdin);
    freopen("blocks.out","w",stdout);
    n=read();m=read();
    for(int i=;i<=n;i++) a[i]=read();
    while(m--) solve(read());
    return ;
}

/*
将字符串倒序插入trie树，问题就转换成了若干字符串结束的LCA深度
倍增维护LCA，每插入一个字符串，处理一次fa数组就可以了
当然这题也可以哈希+二分
*/
#include<iostream>
#include<cstdio>
#include<cstring>

#define N 100007
#define M 1000007

using namespace std;
int Log[N],pos[N];
int n,m,len,cnt,sum;
char last[N],str[N];
struct Trie
{
    int s[],f[];
    int dep;
}tr[M];

inline int read()
{
    int x=,f=;char c=getchar();
    while(c>''||c<''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}

void insert(int x)
{
    last[x]=str[len-];
    int now=;
    for(int i=len-;i>=;i--)
    {
        int id=str[i]-'a';
        if(!tr[now].s[id])
        {
            tr[now].s[id]=++cnt;
            tr[cnt].f[]=now;
            tr[cnt].dep=tr[now].dep+;
            for(int i=;i<=;i++)
            {
                tr[cnt].f[i]=tr[tr[cnt].f[i-]].f[i-];
                if (tr[cnt].f[i]==) break;//再往后跳也不可能有f值.
            }
        }now=tr[now].s[id];
    }pos[x]=now;
}

inline void init()
{
    for(int i=,now=-,next=;i<=N;i++)
    {
        if(i==next) now++,next<<=;
        Log[i]=now;
    }
}

int up(int x,int step)
{
    while (step)
    {
        int up=Log[step];
        x=tr[x].f[up];
        step-=(<<up);
    }
    return x;
}

int LCA(int x,int y)
{
    if(tr[x].dep>tr[y].dep) x=up(x,tr[x].dep-tr[y].dep);
    else y=up(y,tr[y].dep-tr[x].dep);
    if(x== || y==) puts("myjdsb");

    int k=Log[tr[x].dep];
    while(x!=y)
    {
        while(k>= && tr[x].f[k]==tr[y].f[k]) k--;
        if(k==-) return tr[x].f[];
        x=tr[x].f[k];y=tr[y].f[k];
    }return x;
}

int main()
{
    freopen("biology.in","r",stdin);
    freopen("biology.out","w",stdout);
    init();
    n=read();m=read();cnt=;sum=;
    for(int i=;i<=n;i++)
    {
        scanf("%s",str);
        len=strlen(str);
        sum+=len;insert(i);
    }
    while(m--)
    {
        int ty=read();
        if(ty==)
        {
            scanf("%s",str);
            len=strlen(str);
            insert(++n);
        }
        else
        {
            int T=read(),ans=;
            while(T--)
            {
                int x=read();
                if(!ans) ans=pos[x];
                else ans=LCA(ans,pos[x]);
            }
            printf("%d\n",tr[ans].dep);
        }
    }
    return ;
}