深度神经网络多任务学习(Multi-Task Learning in Deep Neural Networks)

https://cloud.tencent.com/developer/article/1118159

http://ruder.io/multi-task/

https://arxiv.org/abs/1706.05098

两种深度学习 MTL 方法

1、Hard 参数共享

在实际应用中，通常通过在所有任务之间共享隐藏层，同时保留几个特定任务的输出层来实现。

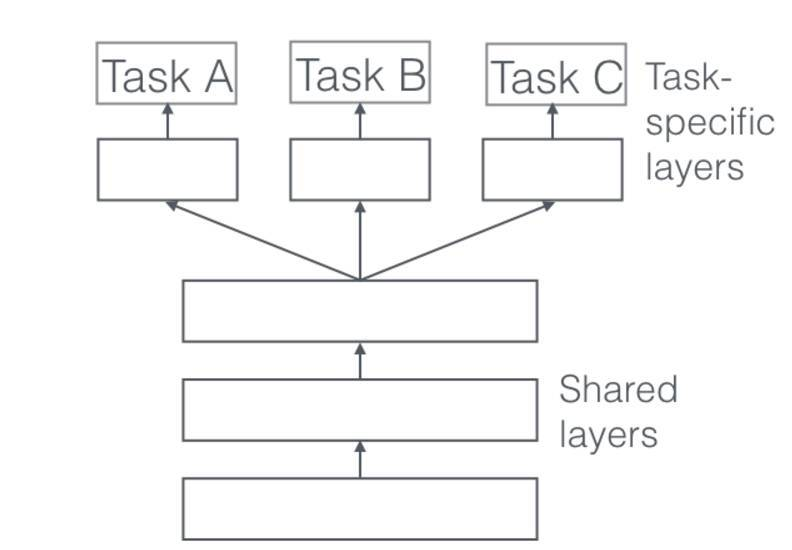
共享 Hard 参数大大降低了过拟合的风险。这很直观：我们同时学习的工作越多，我们的模型找到一个含有所有任务的表征就越困难，而过拟合我们原始任务的可能性就越小。

2、Soft 参数共享

在软参数共享中，每个任务都有单独的模型，每个模型包含各自的参数。模型参数之间的距离会作为正则项来保证参数尽可能相似。

Why does MTL work?

我们假设我们有两个相关的任务A和B，依赖一个共享的隐藏层表示F。

1、Implicit data augmentation

MTL可以有效增加用于模型训练的样本量。由于所有任务难免会有一些噪声，当我们在任务A上训练模型， 我们的目标是学习针对任务A的一个好的表示，可以完全避免依赖数据的噪音，而且泛化效果好。由于不同的任务有不同的噪声模式，一个自动学习两个任务的模型能够学习一个更加泛化的表示。只学习A任务有风险对任务A有过拟合风险，但是把A和B联合起来学习能够通过平均噪声模式使得模型获得一个更好的表示F。

2、Attention focusing

如果一个任务数据中噪声非常多或者数据较少而且高维，模型很难辨别相关特征和不相关特征。由于MTL中其他任务也可以提供辨别特征是否相关的依据，所以可以帮助模型将注意力集中在那些真正起作用的特征上。

3、Eavesdropping

某些特征G对于任务B来说容易学习，但是对于任务A来说较难学习。这可能是因为任务A中特征以更复杂的方式作用或者其他特征阻碍了模型学习G。通过MTL，我们允许模型偷听，也就是说通过任务B来学习G。最简单的方式就是通过hints，也就是直接训练模型来学习最重要的特征。

4、Representation bias

MTL中会使模型偏向于使用其他任务也倾向的表示。这也使得模型在未来的新任务上有更好的泛化能力，因为在足够数量任务上表现较好的假设空间也会在新任务上表现较好，毕竟这些任务都是在相同的环境中。

哪些辅助任务是有帮助的？

在本节中，我们讨论了可用于 MTL 的不同辅助任务，即使我们只关心一个任务。然而，我们仍然不知道什么辅助任务在实际中是有用的。寻找辅助任务主要是基于一种假设，即认为辅助任务与主任务有某种相关性，并且有助于预测主任务。

然而，我们仍然不知道什么时候两个任务应该被认为是相似或相关的。Caruana（1997）定义如果两个任务使用相同的特征作判断，那么这两个任务是相似的。Baxter（2000）认为理论上相关的任务共享一个共同的最优假设类，即具有相同的归纳偏置。[50] 提出，如果两个任务的数据可以使用一个从一组分布变换 F 得到的固定概率分布生成，那么两个任务是 F-相关的。虽然这允许对不同传感器收集的相同分类问题的数据的任务进行推理，例如用不同角度和照明条件的相机得到的数据进行对象识别，这不适用于处理不同问题的任务。Xue 等人（2007）讨论，如果两个任务的分类边界即参数向量接近，则两个任务是相似的。

在理解任务相关性方面，尽管有这些早期的理论进展，但实践中还没有太多进展。任务相似度不是二进制的，而是在一个频谱范围内。MTL 中，更多的相似任务有更大的作用，而较少的相似任务相反。允许我们的模型学习如何分享每个任务，可能使我们能够暂时避开理论的缺失，并更好利用即使是松散相关的任务。然而，我们还需要制定一个有关任务相似性的原则概念，以便了解我们应该选择哪些任务。

最近的工作 [52] 发现了标签满足紧凑且均匀分布的辅助任务，这适用于 NLP 中的序列标签问题，并且已经在实验中（Ruder 等人，2017）得到证实。此外已经发现，主任务更有可能快速达到高峰平稳（plateau），而辅助任务不容易达到高峰平稳 [53]。

然而，这些实验迄今在范围上受到限制，最近的发现仅提供了加深对神经网络中多任务学习理解的启发式线索。