并不对劲的字符串专题（二）：kmp

据说这些并不对劲的内容是《信息学奥赛一本通提高篇》的配套练习。

先感叹一句《信息学奥赛一本通提高篇》上对kmp的解释和matrix67的博客相似度99%（还抄错了），莫非matrix67藏在编者之中？

但这不重要，因为并不对劲的人不会对kmp作出任何解释。

课后练习：

1.bzoj1355->

可以将题目中给出的字符串看成形如这样的串：

那么，对于其中的某一位：

它到当前前缀的第二个循环节的开始组成的子串和前缀相等：

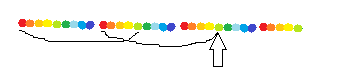
所以，对于当前位置x，fail[x]就是它到当前前缀的第二个循环节的开始组成的子串的长度，x-fail[x]就相当于字符串的开始到当前前缀的第二个循环节的开始的长度，也就是一个循环节的长度：

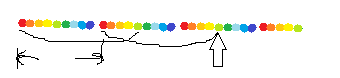
但是，随着x增大，x-fail[x]不降，所以对于长度为n的串，答案就是n-fail[n]。

代码就是求fail指针就行了。

#include<bits/stdc++.h>
using namespace std;
#define maxn 1000010
int fa[maxn],n,ans;
char s[maxn];
int main()
{
    scanf("%d%s",&n,s+1);
    fa[0]=-1,fa[1]=0;ans=1;
    for(int i=2;i<=n;i++)
    {
        int u=i-1;
        while(u&&s[fa[u]+1]!=s[i])u=fa[u];
        if(u)fa[i]=fa[u]+1;
        else fa[i]=0;
    }
    printf("%d",n-fa[n]);
    return 0;
}

　　

2.bzoj1511->

并不能读懂题面，求大佬帮助。

3.bzoj3620->

题目中要找形如A+B+A的子串，所以可以枚举左端点，再算出每个右端点是否可行。

首先，固定左端点后，求出fail指针。对于fail[x]*2<x的，肯定是没问题了（如图）：

对于fail[x]*2>=x的呢？会发现，1到fail[x]的子串和x-fail[x]+1到x的子串一样，1到fail[fail[x]]的子串和fail[x]-fail[fail[x]]+1到fail[x]的子串一样，所以1到fail[fail[x]]的子串和x-fail[fail[x]]+1到x的子串一样。那么就可以顺着fail指针往上找，直到长度*2<x且长度>=k。

不断顺着fail指针往上找的过程听上去很暴力，这题本来就很暴力了，就要避免这种暴力的。发现对于点x求出合法解为y后，对于x在fail树所有子孙，就都是合法的了。那么可以标记x，这样计算x在fail树所有子孙时，走到x就可以停了。

这个优化听上去很扯，它还是O(n²)的，但是15000的数据还是过了，是因为kmp常数小的缘故？

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<stack>
#include<set>
#include<queue>
#define maxn 15010
using namespace std;
int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)&&ch!='-')ch=getchar();
    if(ch=='-')f=-1,ch=getchar();
    while(isdigit(ch))x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*f;
}
void write(int x)
{
    int f=0;char ch[20];
    if(x==0){putchar('0'),putchar('\n');return;}
    if(x<0){putchar('-'),x=-x;}
    while(x)ch[++f]=x%10+'0',x/=10;
    while(f)putchar(ch[f--]);
    putchar('\n');
}
int ans,k,fa[maxn],n,lst[maxn];
char s[maxn];
void rebuild()
{
    for(int i=1;i<n;i++)s[i]=s[i+1];
    n--;
}
int main()
{
    scanf("%s%d",s+1,&k);
    n=strlen(s+1);
    for(;n>=(k<<1|1);)
    {
        fa[1]=0,fa[0]=-1;lst[0]=lst[1]=-1;
        for(int i=2;i<=n;i++)
        {
            lst[i]=-1;
            int u=i-1;
            while(s[fa[u]+1]!=s[i]&&u)u=fa[u];
            if(!u)fa[i]=0;
            else fa[i]=fa[u]+1;
        }
        for(int i=1;i<=n;i++)
        {
            int u=fa[i];
            while((u<<1|1)>i&&fa[u]>=k){if(lst[u]!=-1)u=lst[u];else u=fa[u];}
            //cout<<u<<endl;
            if((u<<1|1)<=i&&u>=k) lst[i]=u,ans++;
            //cout<<lst[i]<<" ";
        }
        //cout<<"+++"<<endl;
        rebuild();
    }
    write(ans);
    return 0;
}
/*
aaaaa
1
*/

　　

4.bzoj3942->

先想一个比较暴力的：让一个指针k从头往后扫S，每次判断长度为|T|的后缀是否等于T。

这个的时间复杂度是O(|S|*|T|)，发现判断长度为|T|的后缀是否等于T有点像kmp。

那么就可以再维护一个指针p，表示T中走到的位置。对于S的每一位，开一个数组记录k走到这里时p走到的位置。

每当p走到T的结尾时，k退回|T|前的位置，p变成之前记录的k走到该点时p的位置。

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<set>
#include<stack>
#include<queue>
#define maxn 1000010
using namespace std;
char s[maxn],t[maxn];
int fa[maxn],mat[maxn],top,ns,nt,ans[maxn];
void go(int & u,char c)
{
    while(t[u+1]!=c){u=fa[u];if(!u)break;}
    if(t[u+1]==c)u++;
    else u=0;
}
int main()
{
    //freopen("censor.in","r",stdin);
    //freopen("censor.out","w",stdout);
    scanf("%s%s",s+1,t+1);
    ns=strlen(s+1),nt=strlen(t+1);
    fa[1]=0;
    for(int i=2;i<=nt;i++)
    {
        int u=i-1;
        while(t[fa[u]+1]!=t[i]&&u)u=fa[u];
        if(!u)fa[i]=0;
        else fa[i]=fa[u]+1;
    }
    int u=0;
    for(int i=1;i<=ns;i++)
    {
        go(u,s[i]);
        mat[i]=u;
        ans[++top]=i;
        if(u==nt)
        {
            top-=nt;
            u=mat[ans[top]];
        }
    }
    //for(int i=1;i<=ns;i++)cout<<mat[i]<<" ";cout<<endl;
    for(int i=1;i<=top;i++)putchar(s[ans[i]]);
    return 0;
}