[UOJ311]积劳成疾

---

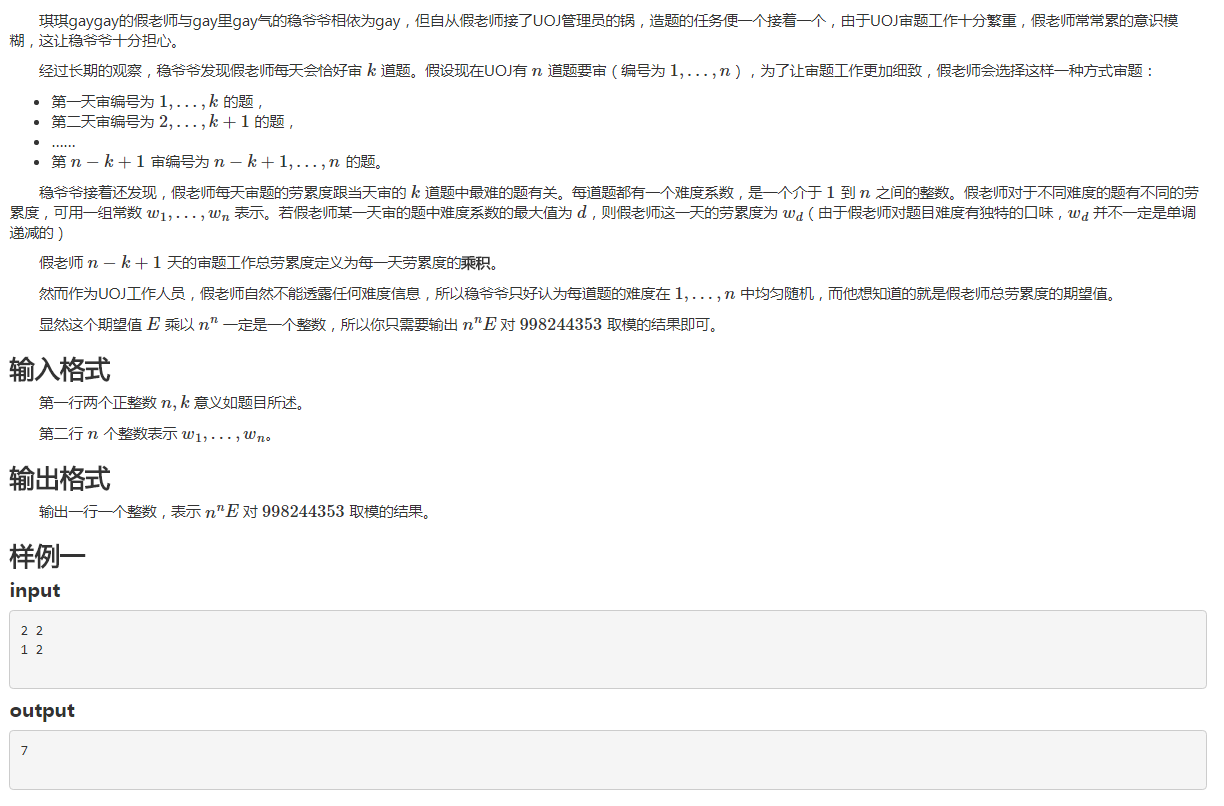
题解

dp

似乎这个最大值不好设计状态啊==

但是可以发现这\(n\)个点每个点都是相同的

可以设计状态\(f_{i,j}\)表示一个长度为\(i\)的一段区间的最大值不会超过\(j\)的价值

那么转移就类似于区间\(DP\),先枚举长度,再枚举最大值,然后再暴力枚举一个位置表示这个最大值最靠右的位置,然后计算这个最大值跨过这个区间的贡献即可

\(f_{i,j}=f_{i,j-1}+\sum_{k=1}^{i}{f_{k-1,j} \times f_{i-k,j - 1} \times p_{j}^{有几个长度为m的区间跨过了这个最大值}}\)

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
const int M = 405 ;
const int mod = 998244353 ;
using namespace std ;

inline int read() {
	char c = getchar() ; int x = 0 , w = 1 ;
	while(c>'9'||c<'0') { if(c=='-') w = -1 ; c = getchar() ; }
	while(c>='0'&&c<='9') { x = x*10+c-'0' ; c = getchar() ; }
	return x*w ;
}

int n , m ;
int val[M][M] , f[M][M] ;

inline int T(int len , int k) {
	int l = max(1 , k - m + 1) , r = min(len , k + m - 1) ;
	return max(r - l - m + 2 , 0) ;
}
int main() {
	n = read() ; m = read() ;
	for(int i = 1 ; i <= n ; i ++) {
		val[i][0] = 1 ; val[i][1] = read() ;
		for(int j = 2 ; j <= n ; j ++)
			val[i][j] = 1LL * val[i][j - 1] * val[i][1] % mod ;
	}
	for(int i = 0 ; i <= n ; i ++) f[0][i] = 1 ;
	for(int i = 1 ; i <= n ; i ++)
		for(int j = 1 ; j <= n ; j ++) {
			f[i][j] = f[i][j - 1] ;
			for(int k = 1 ; k <= i ; k ++)
				f[i][j] = (f[i][j] + 1LL * f[k - 1][j] * f[i - k][j - 1] % mod * val[j][T(i , k)] % mod) % mod ;
		}
	printf("%d\n",f[n][n]) ;
	return 0 ;
}