【C】——幻方算法

一、幻方按照阶数可分成了三类，即奇数阶幻方、双偶阶幻方、单偶阶幻方。

二、奇数阶幻方（劳伯法）

奇数阶幻方最经典的填法是罗伯法。填写的方法是：

把1（或最小的数）放在第一行正中；按以下规律排列剩下的(n×n－1)个数：
（1）每一个数放在前一个数的右上一格；

（2）如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；

（3）如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；

（4）如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在底行且最左列；

（5）如果这个数所要放的格已经有数填入，那么就把它放在前一个数的下一行同一列的格内。

例，用该填法获得的5阶幻方：

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

二、双偶数阶幻方（海尔法）

所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方，即4K阶幻方。在说解法之前我们先说明一个“互补数”定义：就是在n阶幻方中，如果两个数的和等于幻方中最大的数与1的和（即n×n＋1），我们称它们为一对互补数。如在三阶幻方中，每一对和为10的数，是一对互补数 ；在四阶幻方中，每一对和为17的数，是一对互补数。

双偶数阶幻方最经典的填法是海尔法。填写的方法是：

以8阶幻方为例：
（1）先把数字按顺序填。然后，按4×4把它分割成4块（如图）

1	2	3	4	5	6	7	8
9	10	11	12	13	14	15	16
17	18	19	20	21	22	23	24
25	26	27	28	29	30	31	32
33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48
49	50	51	52	53	54	55	56
57	58	59	60	61	62	63	64

（2）每个小方阵对角线上的数字（如左上角小方阵部分），换成和它互补的数。

64	2	3	61	60	6	7	57
9	55	54	12	13	51	50	16
17	47	46	20	21	43	42	24
40	26	27	37	36	30	31	33
32	34	35	29	28	38	39	25
41	23	22	44	45	19	18	48
49	15	14	52	53	11	10	56
8	58	59	5	4	62	63	1

三、单偶数阶幻方（斯特拉兹法）

所谓单偶阶幻方就是当n不可以被4整除时的偶阶幻方，即4K+2阶幻方。如(n=6，10，14……)的幻方。

单偶数阶幻方最经典的填法是斯特拉兹法。填写的方法是：

以10阶幻方为例。这时，k=2。
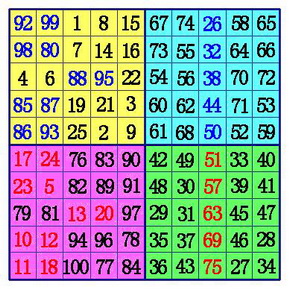
（1）把魔方阵分为A，B，C，D四个象限，这样每一个象限肯定是奇数阶。用罗伯法，依次在A象限，D象限，B象限，C象限按奇数阶幻方的填法填数。

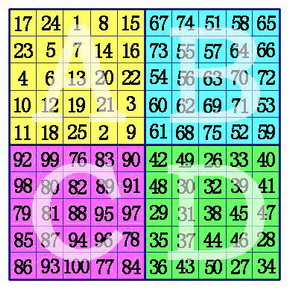
（2）在A象限的中间行、中间格开始，按自左向右的方向，标出k格。A象限的其它行则标出最左边的k格。将这些格，和C象限相对位置上的数互换位置。

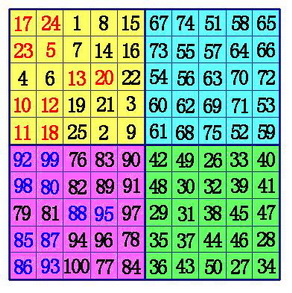
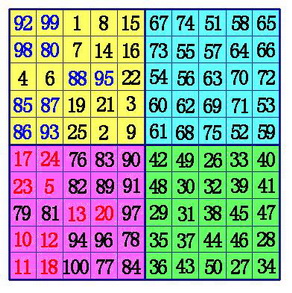
（3）在B象限所有行的中间格，自右向左，标出k－1格。(注：6阶幻方由于k－1=0，所以不用再作B、D象限的数据交换)，将这些格，和D象限相对位置上的数互换位置。

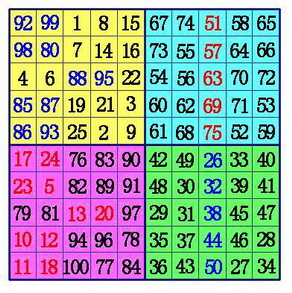
以上内容来源：http://www.cnblogs.com/panlijiao/archive/2012/05/11/2496757.html

实现代码如下：

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>

 #define COL 20
 #define ROW 20

 void deal_argv(int argc, char **argv, int *degree) {
         if (argc != ) {
                 printf("cmd: ./a.out degree\n");
                 exit(-);
         } else {
                 *degree = atoi(argv[]);
                 if (*degree <=  || *degree > ) {
                         printf("the degree is between 3 and 20\n");
                         exit(-);
                 }
         }
 }

 void show_array(int (*array)[ROW], int degree) {
         int row, col;
         for (row = ; row < degree; row++){
                 for (col = ; col < degree; col++)
                         printf("%5d", array[row][col]);
                 printf("\n");
         }
 }

 void init_array(int (*array)[ROW], int size) {
         memset(array, , size);
 }

 void odd_num_magic_square(int degree, int (*array)[ROW], int x, int y, int num) {
         int element = ;
         int col = ;
         int row = degree / ;

         for (element = num; element <= degree * degree + num - ; element++) {
                 array[col + x][row + y] = element;
                 if (array[(col -  + degree) % degree + x][(row + ) % degree + y] != ) {
                         col = (col +  + degree) % degree;
                 } else {
                         row = (row + ) % degree;
                         col = (col -  + degree) % degree;
                 }
         }
 }

 void fill_array(int (*array)[ROW], int degree) {
         int row, col;
         int num = ;

         for (col = ; col < degree; col++)
                 for (row = ; row < degree; row++)
                         array[col][row] = num++;
 }

 void double_magic_square(int degree, int (*array)[ROW]) {
         int complement = ;
         int deg = degree / ;
         int row, col;

         fill_array(array, degree);
         complement = degree * degree + ;

         for (col = ; col < deg; col++) {
                 for (row = ; row < deg; row++) {
                         array[col * ][row * ] = complement - array[col * ][row * ];
                         array[col *  + ][row *  + ] = complement - array[col *  + ][row *  + ];
                         array[col *  + ][row *  + ] = complement - array[col *  + ][row *  + ];
                         array[col *  + ][row *  + ] = complement - array[col *  + ][row *  + ];

                         array[col *  + ][row * ] = complement - array[col *  + ][row * ];
                         array[col *  + ][row *  + ] = complement - array[col *  + ][row *  + ];
                         array[col *  + ][row *  + ] = complement - array[col *  + ][row *  + ];
                         array[col * ][row *  + ] = complement - array[col * ][row *  + ];
                 }
         }
 }

 void change_value(int *value_a, int *value_b) {
         int tmp;
         tmp = *value_a;
         *value_a = *value_b;
         *value_b = tmp;
 }

 void single_magic_square(int degree, int (*array)[ROW]) {
         int deg = degree / ;
         int k = ;
         int row, col;
         int tmp_row = ;

         odd_num_magic_square(deg, array, , , );
         odd_num_magic_square(deg, array, deg, deg, deg * deg + );
         odd_num_magic_square(deg, array, , deg, deg * deg *  + );
         odd_num_magic_square(deg, array, deg, , deg * deg *  + );

         k = (degree - ) / ;
         for (row = ; row < k; row++) {
                 for (col = ; col < deg; col++) {
                         if (col == deg / ) {
                                 change_value(&array[col][deg /  + row], &array[col + deg][deg /  + row]);
                         } else {
                                 change_value(&array[col][row], &array[col + deg][row]);
                         }
                 }
         }

         for (row = ; row < k - ; row++) {
                 for (col = ; col < deg; col++) {
                         tmp_row = row + deg + deg /  +  - k + ;
                         change_value(&array[col][tmp_row], &array[col + deg][tmp_row]);
                 }
         }

 }

 int main(int argc, char *argv[]) {
         int array[COL][ROW];
         int degree = ;

         deal_argv(argc, argv, &degree);

         init_array(array, sizeof(array));
         if ((degree % ) != ) {
                 odd_num_magic_square(degree, array, , , );
                 show_array(array, degree);
         } else if (degree %  == ) {
                 double_magic_square(degree, array);
                 show_array(array, degree);
         } else {
                 single_magic_square(degree, array);
                 show_array(array, degree);
         }

         return ;
 }