hdu acmsteps 2.2.1 Fibonacci

Fibonacci

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 2087 Accepted Submission(s): 999

Problem Description

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

Sample Input

0
1
2
3
4
5
35
36
37
38
39
40

Sample Output

0
1
1
2
3
5
9227
1493
2415
3908
6324
1023

解答：

   1:  #include<iostream>

   2:  #include<cmath>

   3:  using namespace std;

   4:  int fib[21]={0,1};

   5:  int main(){

   6:      double a=-0.5*log10(5.0);

   7:      double b=log10(0.5+sqrt(5.0)/2);

   8:      double c=(1-sqrt(5.0))/(1+sqrt(5.0));

   9:      for(int i=2;i<=20;i++){

  10:          fib[i]=fib[i-1]+fib[i-2];    

  11:      }

  12:      for(int n;cin>>n;){

  13:          if(n<=20){

  14:              int ans=fib[n];

  15:              while(ans>=10000) ans/=10;

  16:              cout<<ans<<"\n";

  17:          }

  18:          else{

  19:              double ans=a+n*b+log10(1+pow(c,n));

  20:              ans-=(int)ans;

  21:              ans=pow(10.0,ans);

  22:              while(ans<1000) ans*=10;

  23:              cout<<(int)ans<<"\n";

  24:          }

  25:      }

  26:  }

.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }

分析：

先看对数的性质,，;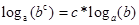
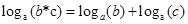假设给出一个数10234432,那么;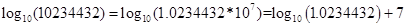
log10(1.0234432)就是log10(10234432)的小数部分.
log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
那么要取几位就很明显了吧~
先取对数(对10取),然后得到结果的小数部分bit,pow(10.0,bit)以后如果答案还是<1000那么就一直乘10。
注意偶先处理了0~20项是为了方便处理~
这题要利用到数列的公式:an=(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)

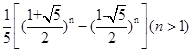
取完对数：

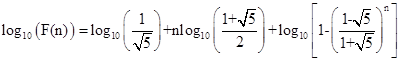
log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)其中f=(sqrt(5.0)+1.0)/2.0;
log10(1-((1-√5)/(1+√5))^n)->0
所以可以写成log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0);
最后取其小数部分。