[NOIP2011] 提高组洛谷P1312 Mayan游戏

题目描述

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个 7 行5 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图6 到图7 ）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图1 和图2）；

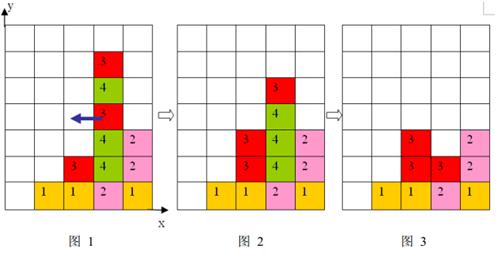
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

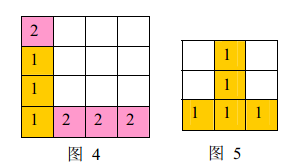
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4 ，三个颜色为1 的方块和三个颜色为 2 的方块会同时被消除，最后剩下一个颜色为 2 的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形，5 个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1 到图 3 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0 ），将位于（3, 3 ）的方块向左移动之后，游戏界面从图 1 变成图 2 所示的状态，此时在一竖列上有连续三块颜色为4 的方块，满足消除条件，消除连续3 块颜色为4 的方块后，上方的颜色为3 的方块掉落，形成图 3 所示的局面。

输入输出格式

输入格式：

输入文件mayan.in，共 6 行。

第一行为一个正整数n ，表示要求游戏通关的步数。

接下来的5 行，描述 7*5 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1 开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式：

输出文件名为mayan.out。

如果有解决方案，输出 n 行，每行包含 3 个整数x，y，g ，表示一次移动，每两个整数之间用一个空格隔开，其中（x ，y）表示要移动的方块的坐标，g 表示移动的方向，1 表示向右移动，-1表示向左移动。注意：多组解时，按照 x 为第一关健字，y 为第二关健字，1优先于-1 ，给出一组字典序最小的解。游戏界面左下角的坐标为（0 ，0 ）。

如果没有解决方案，输出一行，包含一个整数-1。

输入输出样例

输入样例#1：

输出样例#1：

说明

【输入输出样例说明】

按箭头方向的顺序分别为图6 到图11

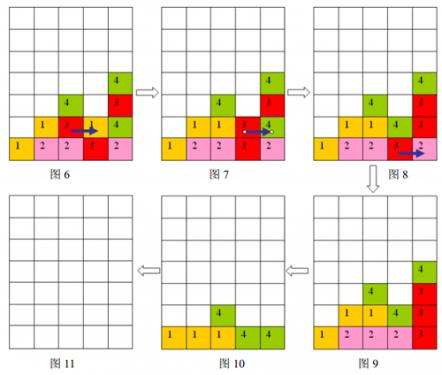
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：（2 ，1 ）处的方格向右移动，（3，1 ）处的方格向右移动，（3 ，0）处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于30% 的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于100%的数据，0 < n≤5 。

noip2011提高组day1第3题

本质上是一道码农题。

掉落和消除的操作都需要模拟，搜索的部分有个重要剪枝——相邻两个块非空，只搜索把左边那个右移（右边那个左移与之等效，但按照规定不是最优解）

 /*by SilverN*/

 #include<algorithm>

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<cmath>

 #include<vector>

 using namespace std;

 const int mx[]={,,,-,};

 const int my[]={,,,,-};

 int ans[][];//答案

 int mp[][];

 int a[][];

 int n;

 void DEBUG(int a[][]){

     int i,j;

     printf("info:\n");

     for(i=;i<=;i++){

         for(j=;j<=;j++) printf("%d ",a[i][j]);

          printf("\n");

     }

     printf("fin\n");

     return;

 }

 bool fall(){//掉落

     bool flag=;

     for(int j=;j<=;++j){

         int i=;

         while(a[i][j]){i++;}

         int tmp=i;

         for(;i<=;i++){

             if(a[i][j]){

                 a[tmp++][j]=a[i][j];

                 a[i][j]=;

                 flag=;

             }

         }

     }

     return flag;

 }

 bool kl[][];

 int BFS(){//消除方块

 //    DEBUG(a);

     memset(kl,,sizeof kl);

     int up,down,left,right,i,j;

     for(i=;i<=;i++)

       for(j=;j<=;j++){

           if(!a[i][j])continue;

           up=down=i;left=right=j;

           while(right< && a[i][right+]==a[i][j])right++;

           while(left> && a[i][left-]==a[i][j])left--;

           while(up< && a[up+][j]==a[i][j])up++;

           while(down> && a[down-][j]==a[i][j])down--;

           if(right-left>=)for(int k=left;k<=right;k++)kl[i][k]=;

           if(up-down>=)for(int k=down;k<=up;k++)kl[k][j]=;

       }

     int flag=;

     for(i=;i<=;++i)

       for(j=;j<=;++j)

           if(kl[i][j])a[i][j]=,flag++;

     if(fall()) flag+=BFS();

 //    printf("flag:%d\n",flag);

     return flag;

 }

 int DFS(int dep,int cnt){

 //    DEBUG(a);

 //    printf("info:%d %d\n",dep,cnt);

     if(dep>n){

         if(!cnt)return ;

         return ;

     }

     int cpy[][];

     memcpy(cpy,a,sizeof a);

     int i,j;

     for(j=;j<=;j++){

         for(i=;i<=;i++){

             if(!a[i][j])continue;

             if(j< && a[i][j]!=a[i][j+]){//右移

                 ans[dep][]=j;ans[dep][]=i;ans[dep][]=;

                 swap(a[i][j],a[i][j+]);

                 int tmp=BFS();

 //                printf("sov1:%d\n",tmp);

                 if(DFS(dep+,cnt-tmp))return ;

                 memcpy(a,cpy,sizeof cpy);

             }

             if(j> && !a[i][j-]){//左移

 //                printf("left:%d %d %d\n",j,i,a[i][j]);

                 ans[dep][]=j;ans[dep][]=i;ans[dep][]=-;

                 swap(a[i][j],a[i][j-]);

                 int tmp=BFS();

 //                printf("sov2:%d\n",tmp);

                 if(DFS(dep+,cnt-tmp))return ;

                 memcpy(a,cpy,sizeof cpy);

             }

         }

     }

     return ;

 }

 void PRT(){

     for(int i=;i<=n;i++)printf("%d %d %d\n",ans[i][]-,ans[i][]-,ans[i][]);

     return;

 }

 int main(){

     scanf("%d",&n);

     int i,j;

     int x,y;

     int num=;

     for(j=;j<=;j++)

       for(i=;scanf("%d",&x) && x;i++)mp[i][j]=x,num++;

     memcpy(a,mp,sizeof mp);

 //    printf("num:%d\n\n",num);

 //    DEBUG(a);

     //

     if(DFS(,num))PRT();

     else printf("-1\n");

     return ;

 }