利用Gabor变换法分析纹理图像 matlab代码实现

Gabor变化属于加窗傅里叶变换，Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。Gabor函数与人眼的生物作用相仿，所以经常用于纹理识别上，并取得了较好的效果。

二维Gobor滤波函数：

​

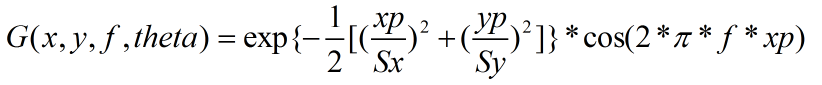
其中：

xp = x*cos(theta)+y*sin(theta)

yp=y*cos(theta)-x*sin(theta)

function [ G,gabout ] = gaborfilter(I,Sx,Sy,f,theta)
% gaborfilter定义，I为输入图像，Sx、Sy是变量在x，y轴变化的范围，即选定的gabor小波窗口的大小
% f为正弦函数的频率，theta为gabor滤波器的方向。G为gabor滤波函数g(x,y)，gabout为gabor滤波后的图像
if isa(I,'double')~=1
    I = double(I);
end
for x = -fix(Sx):fix(Sx)
    for y=-fix(Sy):fix(Sy)
        xp = x * cos(theta) + y * sin(theta);
        yp = y * cos(theta) - x*sin(theta);
        G(fix(Sx)+x+1,fix(Sy)+y+1) = exp(-.5*((xp/Sx)^2+(yp/Sy)^2))*cos(2*pi*f*xp);
    end
end
Imgabout = conv2(I,double(imag(G)),'same');
Regabout = conv2(I,double(real(G)),'same');
gabout = sqrt(Imgabout.*Imgabout+Regabout.*Regabout);  %gabor小波变换后的图像gabout
end

close all;clear all;clc;
I = imread('wenli.jpg');
I=rgb2gray(I);
[G,gabout]=gaborfilter(I,2,4,16,pi/10);  %调用garborfilter()函数对图像做小波变换
J = fft2(gabout);  %对滤波后的图像做fft变换（快速傅里叶），变换到频域
A = double(J);
[m,n] = size(A);
B = A;
C = zeros(m,n);
for i=1:m-1
    for j=1:n-1
        B(i,j) = A(i+1,j+1);
        C(i,j) = abs(round(A(i,j)-B(i,j)));
    end
end
h = imhist(mat2gray(C))/(m*n);
mean = 0;con=0;ent=0;
for i=1:256   %图像的均值，对比度和熵
    mean = mean+(i*h(i))/256;
    con = con+i*i*h(i);
    if(h(i)>0)
        ent = ent-h(i)*log2(h(i));
    end
end
figure;
subplot(121);imshow(I);
subplot(122);imshow(uint8(gabout));
mean,con,ent

​左图为原图，右图为gabor pi/10 方向上处理纹理图像

​左图为原图，右图为gabor pi/4 方向上处理纹理图像

	mean（平均值）	Con（对比度）	Ent（熵）
theta=pi/10	0.0043	1.6111	0.4046
theta=pi/4	0.0042	1.5869	0.3623

熵反映了图像的能量，当滤波器的方向和图像纹理方向越吻合，输出图像的能量越大。这证明了Gabor函数可以捕捉到相当多的纹理信息，具有极佳的空间特征。