基础遗传算法的TSP问题

一、简介

旅行商问题是一个经典的组合优化问题。一个经典的旅行商问题可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。

TSP问题可以分为对称和不对称。在对称TSP问题中，两座城市之间来回的距离是相等的，形成一个无向图，而不对称TSP则形成有向图。对称性TSP问题可以将解的数量减少了一半。所以本次实验的TSP问题使用att48数据，可在tsplib中下载数据包。

遗传算法是一类模拟自然界遗传进化规律的仿生学算法，它不是一个具体的算法，而是一个算法簇。遗传算法是演化算法的一个分支，由于遗传算法的整体搜索策略和优化计算是不依赖梯度信息，所以它的应用比较广泛。我们本次实验同样用到了遗传算法（用MATLAB编写）来解决TSP问题。
二、算法流程图

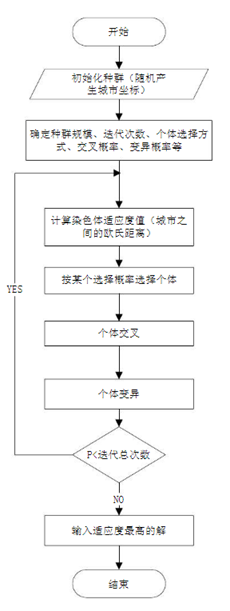
三、关键代码

1.交叉操作

(a) 交叉前：

(b) 交叉后：

%交叉操作函数 cross.m
function [A,B]=cross(A,B)
L=length(A);
if L<10
W=L;
elseif ((L/10)-floor(L/10))>=rand&&L>10
W=ceil(L/10)+8;
else
W=floor(L/10)+8;
end
%%W为需要交叉的位数
p=(L-W+1);%随机产生一个交叉位置
%fprintf('p=%d ',p);%交叉位置
for i=1:W
x=find(A==B(1,p+i-1));
y=find(B==A(1,p+i-1));
[A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1));
[A(1,x),B(1,y)]=exchange(A(1,x),B(1,y));
end

end

2.变异函数

%变异函数 Mutation.m

function a=Mutation(A)
index1=0;index2=0;
nnper=randperm(size(A,2));
index1=nnper(1);
index2=nnper(2);
%fprintf('index1=%d ',index1);
%fprintf('index2=%d ',index2);
temp=0;
temp=A(index1);
A(index1)=A(index2);
A(index2)=temp;
a=A;

end

3.适应度函数

%适应度函数fit.m，每次迭代都要计算每个染色体在本种群内部的优先级别，类似归一化参数。越大约好！
function fitness=fit(len,m,maxlen,minlen)
fitness=len;
for i=1:length(len)
fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m;
end

四、参数对实验的影响

1.城市数量对结果的影响

N=25

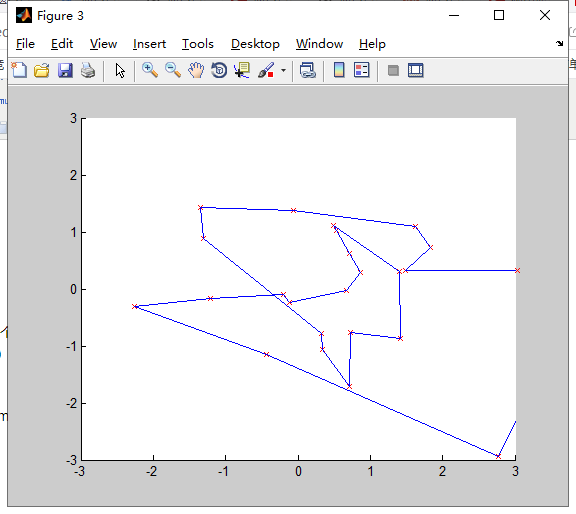
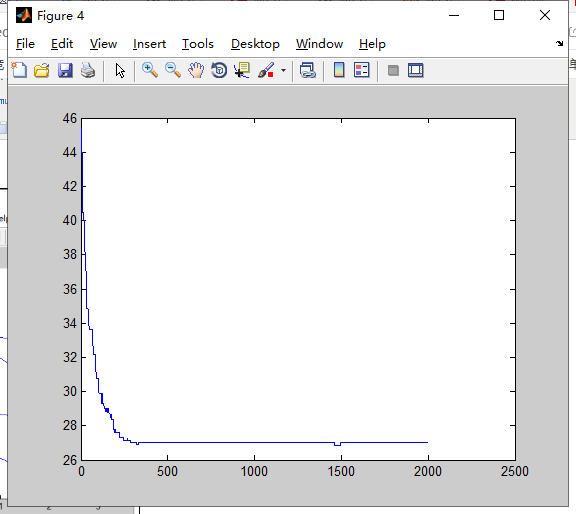
N=50

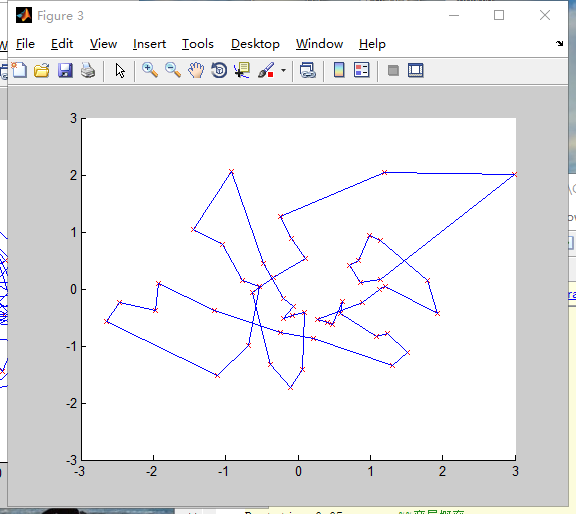
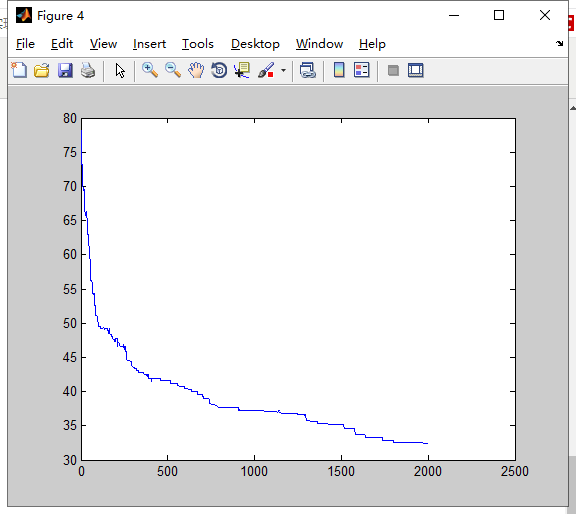
N=100

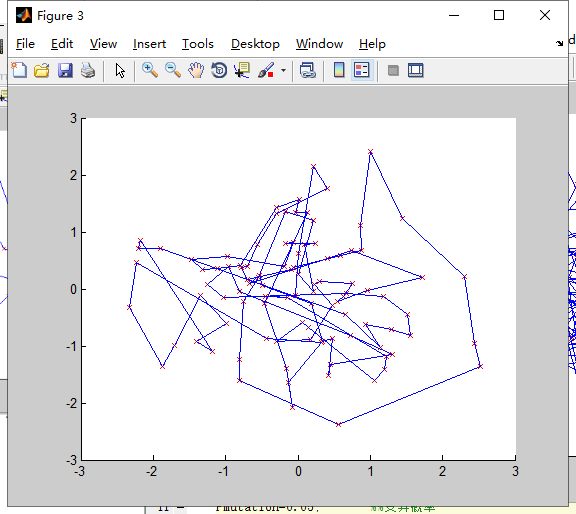
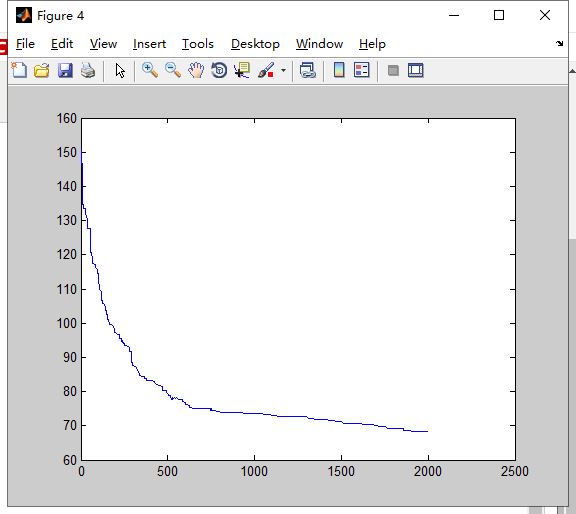
2.种群规模对结果的影响

M=50

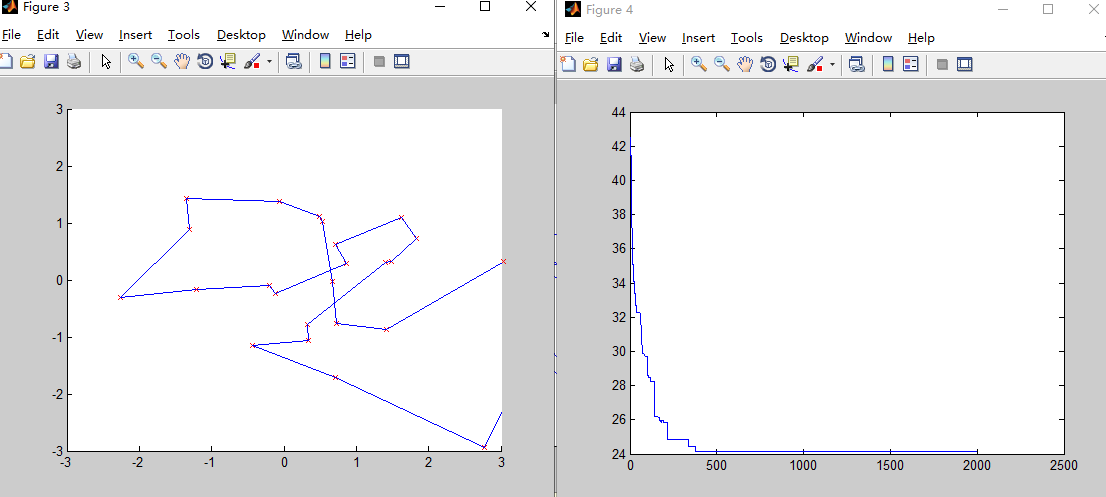
M=80

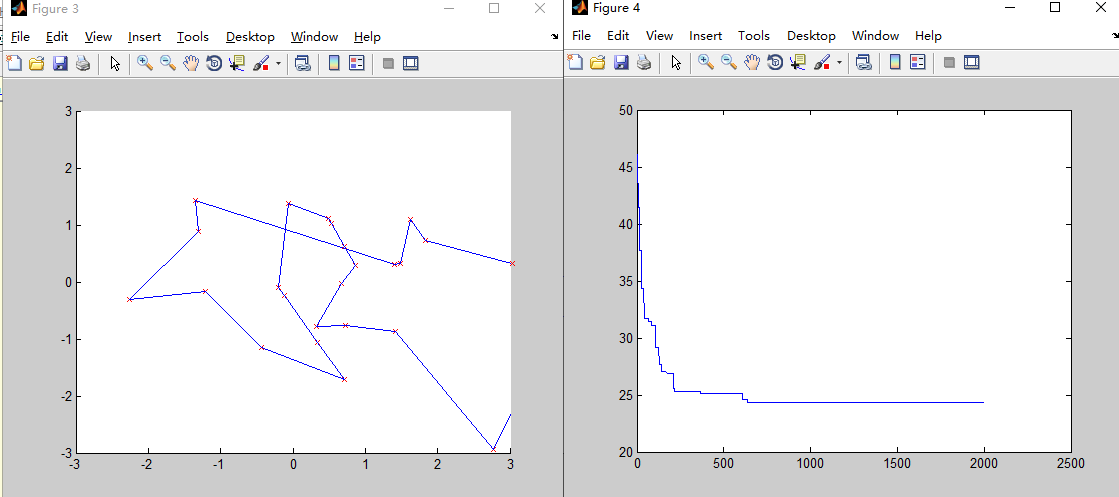
M=100

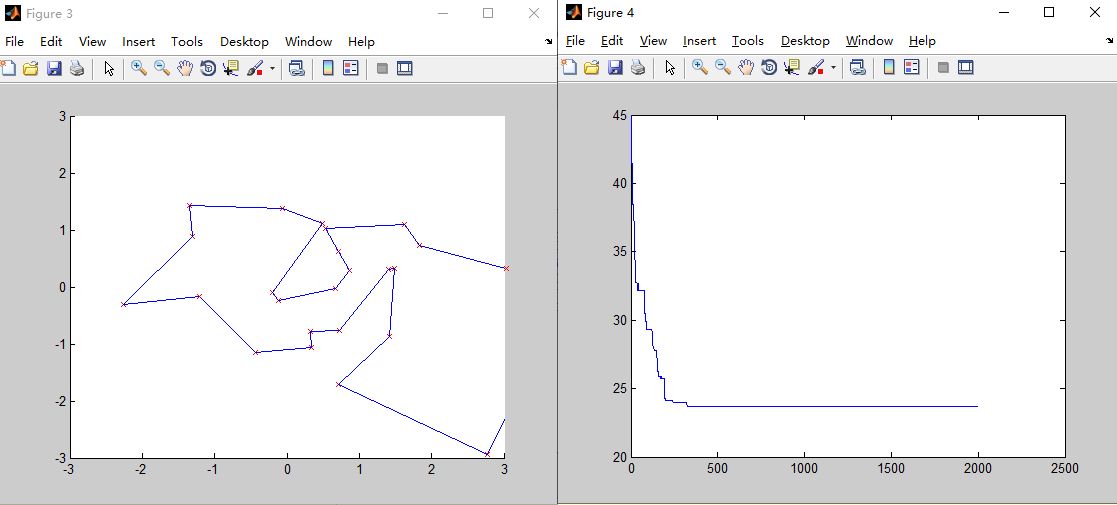
3.交叉概率对结果的影响啊

pc=0.4

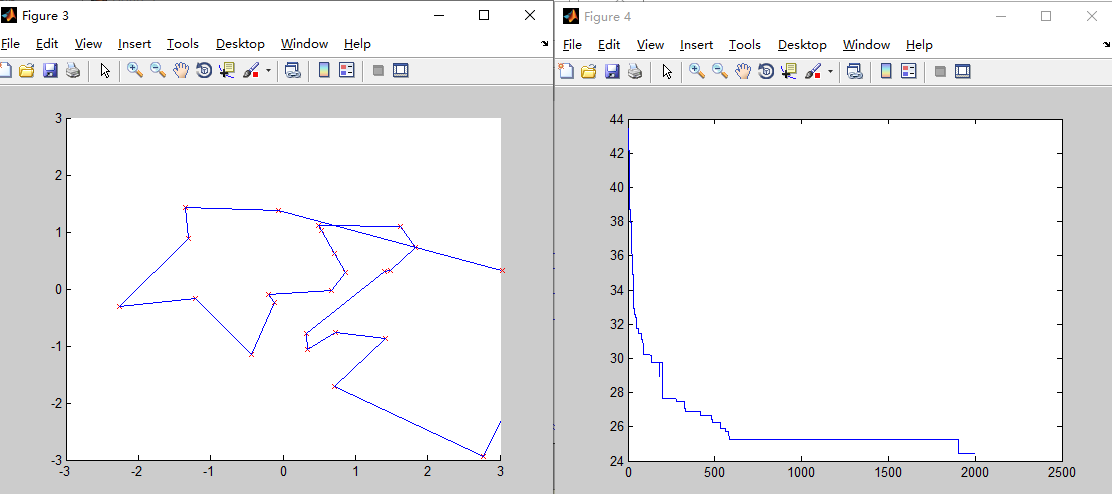
pc=0.6

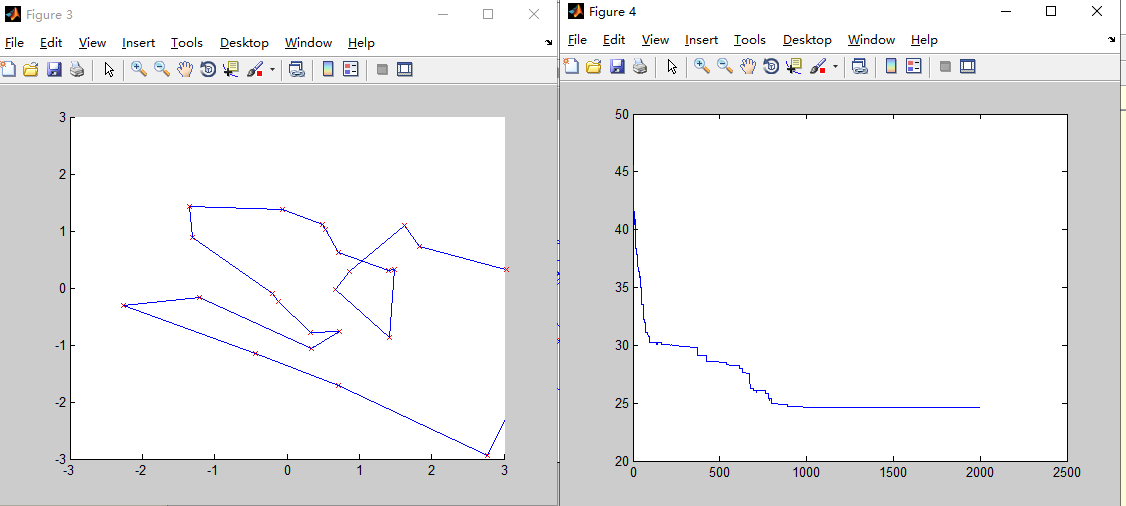
pc=0.8

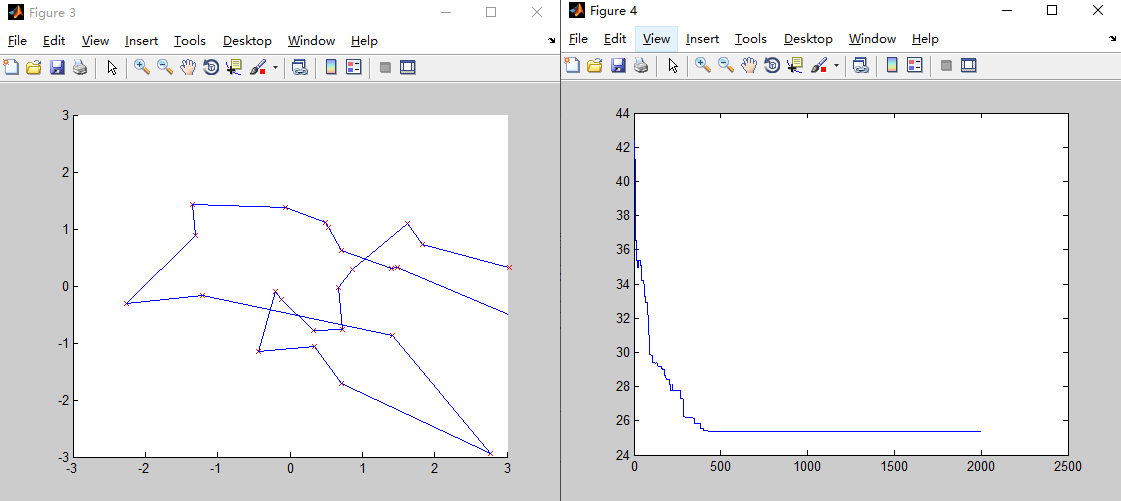
4.变异概率对结果的影响

Pm=0.05

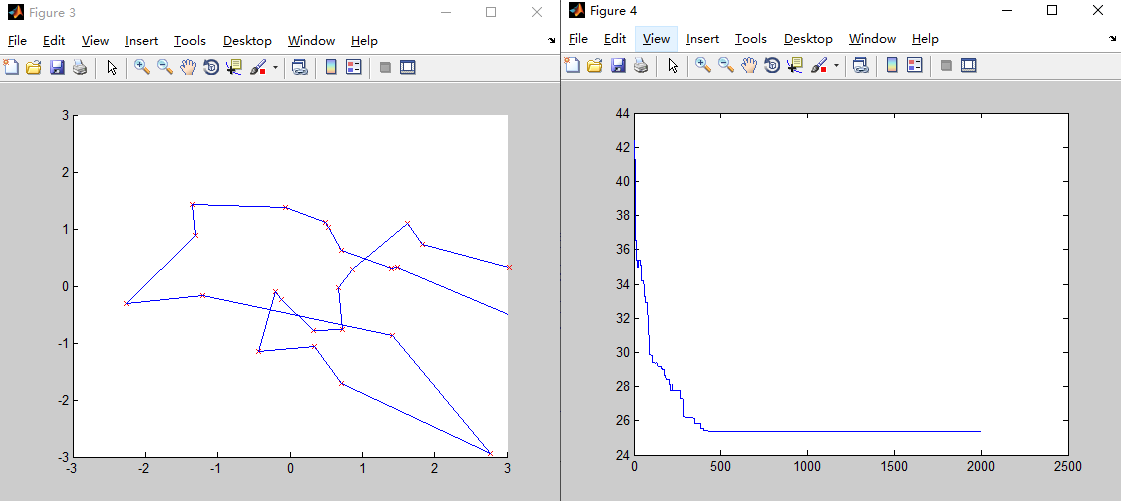
Pm=0.1

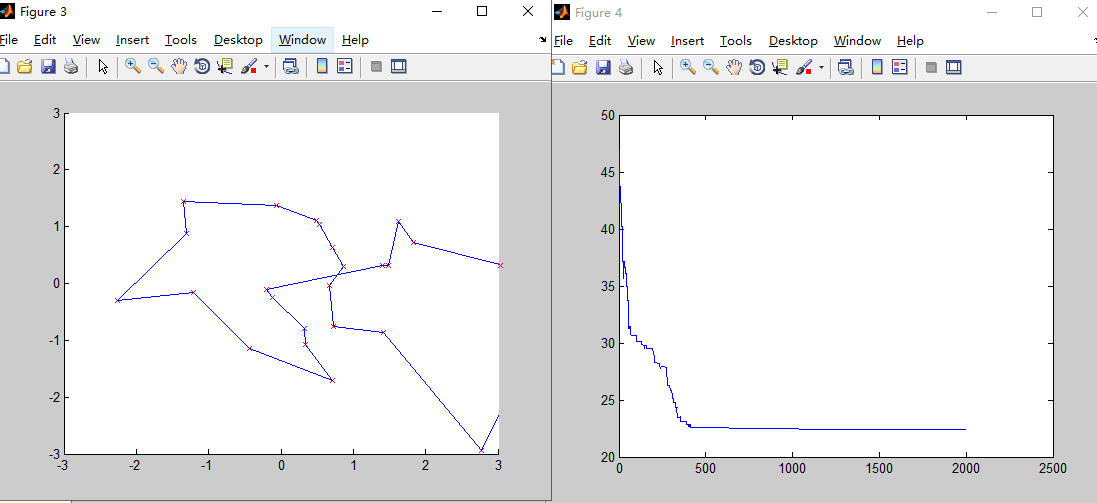
Pm=0.15

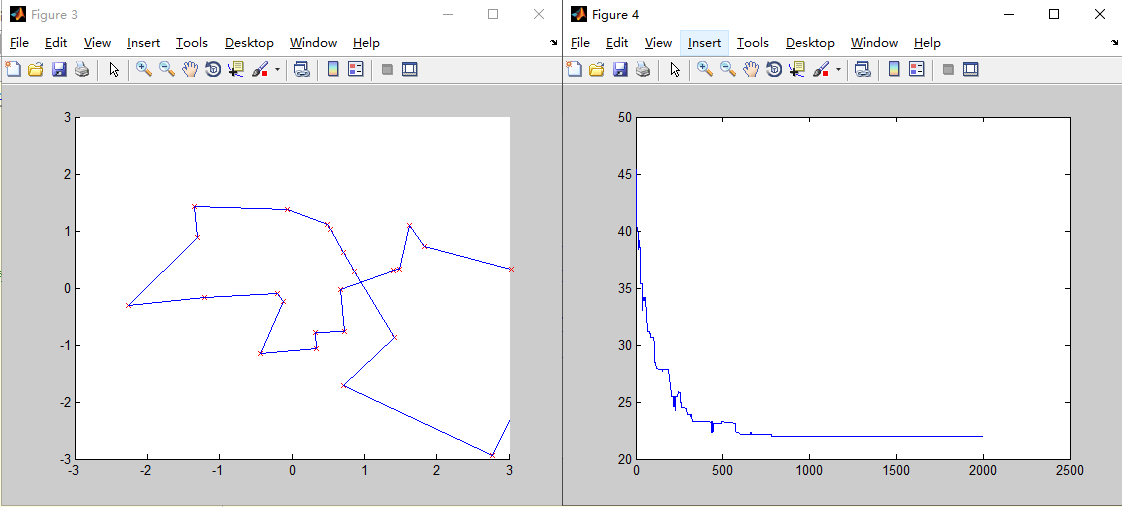
结论：1.城市数量越大，越难以得到最优解。数量越大时应调整其他参数的值才可能得到最优解

　　　 2.Pc, Pm的值减小时，随机性减小，算子中的“择优”功能（如轮盘赌方法）发挥作用更大，所以收敛性较好。Pc，Pm过大也难以得到最优解

           3.种群数量过小，收敛速度较快，容易陷入局部最优，难以得到全局最优解

4.种群规模越大算法结果越精确，适应度越好，但是运行时间越久。