luogu 4211

题意

存在一棵树，每次询问 \(l, r, z\)

求

\[\sum_{i = l} ^ {r} deep(lca(i, z))
\]

---

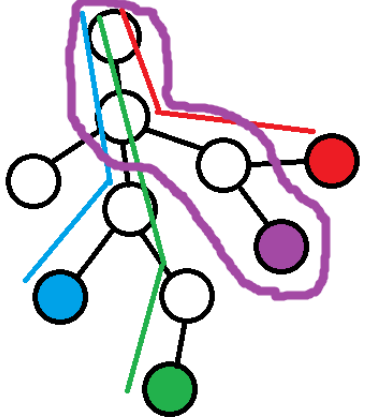
考虑 lca 的实质：两点到根的路径的交集中深度最大的点

其中一点到根的路径上经过的存在于另一点到根的路径上的点一定存在于 lca 到根的路径上

这样的话，对 \([l, r]\) 内的每个点，在其到根的路径上的权 + 1;

查询答案时，就是询问 \(z\) 到根节点的价值和

统计答案是有个小技巧

首先将所有的询问的 \(l, r\) 存到数组中,从小到大扫

如果是某个询问的左端点，查询并记录

如果是右端点，查询，减去相应的左端点就是该询问的答案

---

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <string>

using namespace std;

const int N = 5e4 + 10;
const int Mod = 201314;

#define LL long long

#define int long long

int topp[N], fa[N], size[N], son[N], deep[N], tree[N];
int Tree;
LL W[N << 2], F[N << 2], S[N << 2];
struct Node {int u, v, nxt;} G[N << 1];
int now, head[N];
int n, q;
struct Node_ {
	int l, r, z, id;
} Ask[N];

struct Node_2 {
	int l, opt, id;
} Ask2[N << 1];

#define gc getchar()

inline int read() {
    int x = 0; char c = gc;
    while(c < '0' || c > '9') c = gc;
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc;
    return x;
}

void Link(int u, int v) {G[++ now].v = v; G[now].nxt = head[u]; head[u] = now;}

void Dfs_1(int u, int f_, int dep) {
    fa[u] = f_, deep[u] = dep, size[u] = 1;
    for(int i = head[u]; ~ i; i = G[i].nxt) {
        int v = G[i].v;
        if(v == f_) continue;
        Dfs_1(v, u, dep + 1);
        size[u] += size[v];
        if(size[son[u]] < size[v]) son[u] = v;
    }
}

void Dfs_2(int u, int tp) {
    topp[u] = tp, tree[u] = ++ Tree;
    if(!son[u]) return ;
    Dfs_2(son[u], tp);
    for(int i = head[u]; ~ i; i = G[i].nxt) {
        int v = G[i].v;
        if(v != fa[u] && v != son[u]) Dfs_2(v, v);
    }
}

#define lson jd << 1
#define rson jd << 1 | 1

void Build_tree(int l, int r, int jd) {
	S[jd] = r - l + 1;
	if(l == r) return ;
	int mid = (l + r) >> 1;
	Build_tree(l, mid, lson), Build_tree(mid + 1, r, rson);
}

void Push_down(int jd) {
	(F[lson] += F[jd]) %= Mod, (F[rson] += F[jd]) %= Mod;;
	(W[lson] += S[lson] * F[jd]) %= Mod, (W[rson] += S[rson] * F[jd]) %= Mod;
	F[jd] = 0;
}

void Sec_G(int l, int r, int jd, int x, int y, int opt) {
	if(x <= l && r <= y) {
		(F[jd] += opt) %= Mod;
		(W[jd] += S[jd] * opt) %= Mod;
		return ;
	}
	if(F[jd]) Push_down(jd);
	int mid = (l + r) >> 1;
	if(x <= mid) Sec_G(l, mid, lson, x, y, opt);
	if(y > mid)  Sec_G(mid + 1, r, rson, x, y, opt);
	W[jd] = W[lson] + W[rson];
}

void Sec_G_imp(int x, int opt) {
	int tpx = topp[x];
	while(tpx != 1) {
		Sec_G(1, n, 1, tree[tpx], tree[x], opt);
		x = fa[tpx], tpx = topp[x];
	}
	Sec_G(1, n, 1, tree[1], tree[x], opt);
}

int ret;

void Sec_A(int l, int r, int jd, int x, int y) {
	if(x <= l && r <= y) {
		(ret += W[jd]) %= Mod;
		return ;
	}
	if(F[jd]) Push_down(jd);
	int mid = (l + r) >> 1;
	if(x <= mid) Sec_A(l, mid, lson, x, y);
	if(y > mid)  Sec_A(mid + 1, r, rson, x, y);
}

inline int Sec_A_imp(int x) {
	int tpx = topp[x];
	ret = 0;
	while(tpx != 1) {
		Sec_A(1, n, 1, tree[tpx], tree[x]);
		x = fa[tpx], tpx = topp[x];
	}
	Sec_A(1, n, 1, tree[1], tree[x]);
	return ret % Mod;
}

int Answer[N];
int PreSum[N];

inline bool Cmp(Node_2 a, Node_2 b) {
	return a.l < b.l;
}

main() {
	n = read(), q = read();
	for(int i = 1; i <= n; i ++) head[i] = -1;
	for(int i = 1; i < n; i ++) {
		int u = read() + 1;
		Link(u, i + 1), Link(i + 1, u);
	}
	Dfs_1(1, 0, 1);
	Dfs_2(1, 1);
	Build_tree(1, n, 1);
	for(int i = 1; i <= q; i ++)
		Ask[i].l = read() + 1, Ask[i].r = read() + 1, Ask[i].z = read() + 1, Ask[i].id = i;
	int js = 0;
	for(int i = 1; i <= q; i ++) {
		Ask2[++ js].l = Ask[i].l - 1; Ask2[js].id = i; Ask2[js].opt = 1;
		Ask2[++ js].l = Ask[i].r; Ask2[js].id = i; Ask2[js].opt = 0;
	}
	sort(Ask2 + 1, Ask2 + js + 1, Cmp);
	int L = 0;
	for(int i = 1; i <= js; i ++) {
		while(L < Ask2[i].l) {
			L ++;
			Sec_G_imp(L, 1);
		}
		if(Ask2[i].opt == 1) {
			PreSum[Ask2[i].id] = Sec_A_imp(Ask[Ask2[i].id].z);
		} else {
			Answer[Ask2[i].id] = Sec_A_imp(Ask[Ask2[i].id].z);
			Answer[Ask2[i].id] -= PreSum[Ask2[i].id];
			(Answer[Ask2[i].id] += Mod) %= Mod;
		}
	}
	for(int i = 1; i <= q; i ++) cout << Answer[i] << "\n";
	return 0;
}