T2695 桶哥的问题——吃桶 题解

校内测试 ------T3

对于这个题，首先想到的应该就是暴力枚举了吧，看看数据范围，60就是白送的啦！（但是我也不知道怎么才20分qwq）

思路分析：

这个题要你求所有套餐的总价值，先看一眼产生套餐的条件：

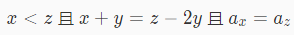
让我们对x+y=z-2y这个式子进行化简：

x+y=z-2y   =>   x+3y=z   =>   z-x=3y

产生的价值为：

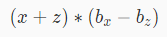
我们可以注意到y对产生的价值的贡献为0（就是说跟y没什么关系），所以上面的式子其实我们知不知道y也就无所谓了，知道了也没什么用，还不如不知道qwq。

化简之后，我们可以重新来定义一下产生套餐的条件了：

x<z且（z-x）%3=0且

所以暴力的同学就不用开三重循环啦，两重就够了qwq。

之前的悲惨代码qwq，跑得超慢，差不多7s：

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n,m,ans;
const int mod=;
int a[],b[];
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++) b[i]=read()%mod;
    for(int i=;i<=n;i++) a[i]=read();
    for(int x=;x<=n;x++)
    {
        for(int z=x;z<=n;z+=)
        {
            if(z==x) continue;
            if(a[z]==a[x])
            ans+=(x+z)*(b[x]-b[z])%mod;
        }
    }
    cout<<(ans+mod)%mod;
    return ;
}

然后，rqy神仙讲了一个O（n）的算法，直接从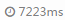降到了！！！不愧是大佬，在这里%一下。

讲下rqy的思路：

跟上面不同的是，我们套餐的价格不再是按照上面的公式求了，而是把它展开：

（x+z）*（bx-bz）=xbx-xbz+zbx-zbz

 我们从1～n枚举每一个z，那么对于z前面的所有下标相差3的整数倍且与z同种的x都可以与z产生一个套餐，那么ans都要加一下上面的那个公式；

我们先假设我们枚举到的这个z它的前面有3个符合条件的x，分别记为x1，x2，x3

x1与z产生的套餐的价值为：（x1+z）*（bx1-bz）=x1bx1-x1bz+zbx1-zbz

x2与z产生的套餐的价值为：（x2+z）*（bx2-bz）=x2bx2-x2bz+zbx2-zbz

x3与z产生的套餐的价值为：（x3+z）*（bx3-bz）=x3bx3-x3bz+zbx3-zbz

那么对于当前这个z，它能产生的价值就是：（x1bx1-x1bz+zbx1-zbz）+（x2bx2-x2bz+zbx2-zbz）+（x3bx3-x3bz+zbx3-zbz）；

我们将它进行合并同类项，得到：（x1bx1+x2bx2+x3bx3）-bz（x1+x2+x3）+z（bx1+bx2+bx3）-zbz*3；

我们可以将这个式子进行推广，假设z前面有n的符合条件的x，那么当前这个z能产生的总价值就是：

（x1bx1+x2bx2+x3bx3+……+xnbxn）-bz（x1+x2+x3+……xn）+z（bx1+bx2+bx3+……+bxn）-zbz*n；

=∑（xbx）-bz*∑（x）+z*（∑bx）-zbz*∑1  （∑1就是符合条件的x的个数）

这个公式就是这个O（n）算法的核心！！！

所以对于当前z，我们只要求出它前面的∑（xbx），∑（x），∑bx，∑1，那么z产生的总价值我们就可以O（1）算出，再加上我们枚举的范围是1～n，所以这个算法的复杂度为O（n）！

但是，怎么求那上面的那几个∑呢？

问得好！我们开数组来分别存上面的几个∑的值，注意这几个数组的下标都是种类：

sx[100005]       //表示前面x下标的总和；∑（x）

sbx[100005]     //表示前面x的美味值的总和；∑bx

sxbx[100005]   //表示前面x的下标乘美味值的总和；∑（xbx）

s[100005]        //表示前面x的个数；∑1

首先我们要解决x和z下标差3的倍数的问题，这个好弄，将mod（3）=0的存为一类，mod（3）=1的存为一类，mod（3）=2的存为一类，那么对于每一类它们的下标相差一定是3的倍数；

然后我们要解决x和z要属于同一种的问题，这就要用到了我们之前把数组的下标定位种类的原理了：

我们将每一种类的桶的∑都存在了数组里面，所以我们只要找和z种类相同的就行了，ans更新如下：

            ans=(ans+sxbx[a[z]])%mod;
            ans=(ans-z%mod*b[z]%mod*s[a[z]]%mod)%mod;  //这里多mod几遍，可能会爆int
            ans=(ans+z*sbx[a[z]]%mod)%mod;
            ans=(ans-b[z]*sx[a[z]]%mod)%mod;

更新完ans之后，对于以后的Z，当前的z也有可能成为x，所以我们要让z更新一下和z属于同一种的∑：

            sxbx[a[z]]=(sxbx[a[z]]+z*b[z]%mod)%mod;
            s[a[z]]=(s[a[z]]+)%mod;
            sbx[a[z]]=(sbx[a[z]]+b[z])%mod;
            sx[a[z]]=(sx[a[z]]+z)%mod;

到这里，就做完了，完整代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
int a[],b[],sxbx[],sx[],sbx[],s[];
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n,m;
long long ans;
const int mod=;
int main()
{
    n=read();
    m=read();
    for(int i=;i<=n;i++) b[i]=read()%mod;             //种类a，美味值b
    for(int i=;i<=n;i++) a[i]=read();
    ans=;
    for(int c=;c<=;c++)                              //一共三类：mod(3)=1 / 2 / 3
    {
        memset(sxbx,,sizeof(sxbx));                   //千万不要忘了清零，防止对其他类的影响
        memset(s,,sizeof(s));
        memset(sbx,,sizeof(sbx));
        memset(sx,,sizeof(sx));
        for(int z=c;z<=n;z+=)                         //解决下标差3的倍数的问题
        {
            ans=(ans+sxbx[a[z]])%mod;                  //更新ans值，注意要和z同种
            ans=(ans-z%mod*b[z]%mod*s[a[z]]%mod)%mod;  //这里多mod几遍，可能会爆int
            ans=(ans+z*sbx[a[z]]%mod)%mod;
            ans=(ans-b[z]*sx[a[z]]%mod)%mod;
            sxbx[a[z]]=(sxbx[a[z]]+z*b[z]%mod)%mod;    //加上z的贡献，注意要和z同种
            s[a[z]]=(s[a[z]]+)%mod;
            sbx[a[z]]=(sbx[a[z]]+b[z])%mod;
            sx[a[z]]=(sx[a[z]]+z)%mod;
        }
    }
    cout<<(ans+mod)%mod;                               //防止答案为负数
    return ;
}

考试有很多大佬比如ybr大佬没有发挥好，才让本蒟蒻rank 6的qwq。