CF1654E Arithmetic Operations 题解

摘自我的洛谷博客。

题目让我们求改变数字的最少次数，那我们转化一下，

求可以保留最多的数字个数 \(cnt\)，再用 \(n\) 减一下就行，即 \(res = n - cnt\)。

我们先考虑两种暴力方法。

第一种暴力方法：

大体思路：因为要保留的最多，那么我们肯定要在众多等差数列中找能对应数字最多的那一个并保留下来。

首先，我们要知道一个概念。

对于这道题，那么我们可以暴力枚举公差 \(d\)（就是数组中相邻两项的差值都是 \(d\)，并把题目中的每个 \(a[i]\) 对应的等差数列的最后一项 \(a[i] + d \times (n - i)\) 计算出来。

---

对于同一个公差 \(d\)，如果不同位置计算出来的序列的最后一个值相同，那就说明它们属于同一个等差数列。

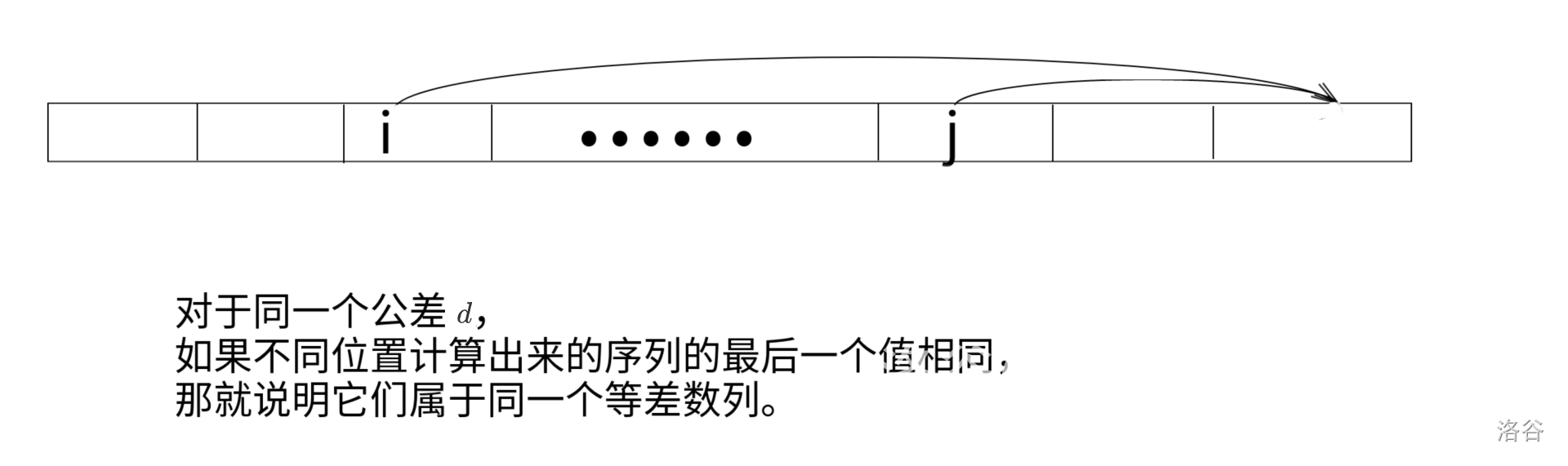
如果有 \(x\) 个数字计算出来的最后一个值都相同，那么采用其对应的等差数列作为修改后的数组，这 \(x\) 个数字是不需要改变的，只需要改变 \(n - x\) 个数字。

那我们可以想到，用桶记录计算出来的值 \(x\) 的出现次数 \(a[x]\)。如果某一次计算出来的值为 \(x\)，那么可以将 \(a[x]\) 加 \(1\)。

如果 \(a[x]\) 是 \(a\) 中最大的元素，那么说明，以 \(a[x]\) 为结尾的等差数列中存在的元素数量最多，那么更改数字的数量也就减少了，只需要 \(n - a[x]\) 个元素。

这种方法的时间复杂度为 \(O(DN)\)，\(D\) 为需要枚举的公差数量。

第二种暴力方法：

考虑动态规划，设 \(f[i][j]\) 表示以 \(a[i]\) 为等差数列最后一个元素的以 \(j\) 为公差的等差数列最多可以保留的数字个数。

我们可以枚举上一个数字 \(a[k]\)，如果它与 \(a[i]\) 在同一等差数列，那么有 \(f[i][j] = f[k][j] + 1\)，表示又可以多保存一个数字了。

那这个序列的公差是多少呢？

这样考虑，中间有 \(i - k\) 个公差，差了 \(a[i] - a[k]\)，那么公差就是\(\frac{a[i] - a[k]}{i - k}\)。

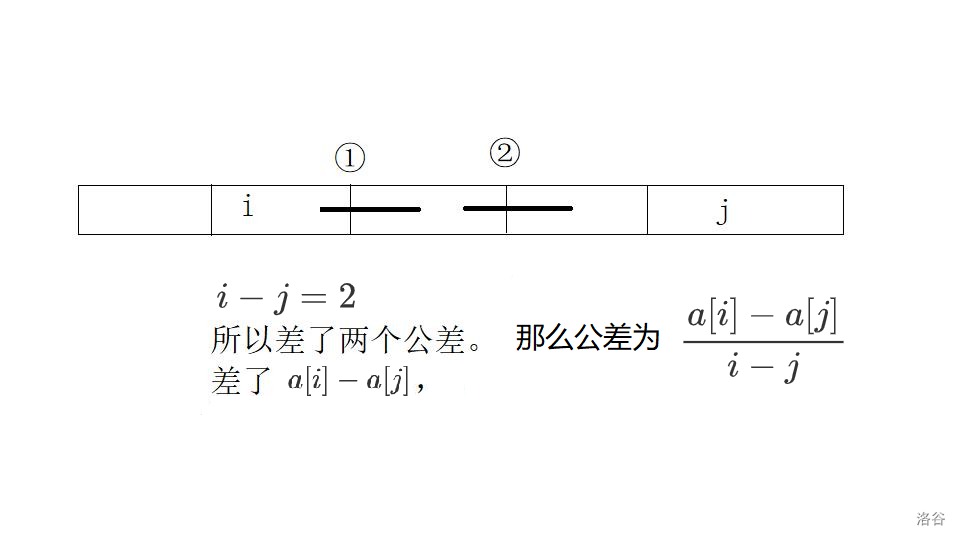
如果除不尽怎么办呢，那么这就说明 \(a[i]\) 和 \(a[k]\) 不能在同一个等差数列，不然公差为小数！

那 \(k\) 从哪里开始枚举呢？从 \(1\) 开始是不是太慢了？

这个等会儿讲。

---

那么为了平衡这两种暴力算法，我们可以这样办：

取输入的数列 \(a\) 的最大值 \(m\)。

我们只使用第一种方法枚举 \([0, \sqrt m]\) 的部分，时间复杂度为 \(O(n \sqrt m)\)。

我们使用第二种方法枚举 \([\sqrt m + 1, n]\) 的部分。

下面探讨第二种方法的时间复杂度，

首先回归到前面的问题，来探讨 \(k\)（\(i\) 的上一位数字在哪里） 从何处开始枚举，到哪里。

到哪里好解决，就是 \(i - 1\)。

而开始的地方，是 \(i - \sqrt m\)。为啥呢？

首先，因为公差 \(D\) 在 \([\sqrt m + 1, n]\) 之间，所以 \(D > \sqrt m\)，那么我们计算差值 \(a[i] - a[k] = (a[k] + (i - k) \times D) - a[k] = (i - k) \times D > (i - k) \times \sqrt m\)。

首先假设 \(i, k\) 都在同一个等差数列中，如果 \(k+ \sqrt m < i\)，那么\(a[i] - a[k] > (i - k) \times \sqrt m > \sqrt m \times \sqrt m = m\)，这样的话，两数之差竟然比 \(m\) 还要大，不成立，

所以 \(k + \sqrt m \geq i\)，也就是说 \(k\) 要从 \(i - \sqrt m\) 开始枚举。

所以，第二种方法的时间复杂度为 \(O(n \sqrt m)\)。

那么这个题的时间复杂度就为 \(O(n \sqrt m)\)。

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <unordered_map>

using namespace std;

const int N = 100010;

int n;
int a[N], maxx, sqrtmaxx;

int u[(int)(N + N * sqrt(N))];                        // 第一种暴力方法的桶
unordered_map<int, int> f[N];                // 第二种暴力方法的动态规划数组。

int max_keep() {
    int ans = 0;
    for (int d = 0; d <= sqrtmaxx; d++) {    // 第一种暴力方法，枚举公差 D
        for (int i = 1; i <= n; i++) {
            ans = max(ans, ++u[a[i] + (n - i) * d]);
        }
        for (int i = 1; i <= n; i++) {
            u[a[i] + (n - i) * d]--;
	}
    }

    for (int i = 1; i <= n; i++) {                         // 第二种暴力方法，动态规划
        for (int j = max(1, i - sqrtmaxx); j < i; j++) {// j只用从 i - sqrt(m) 开始枚举
            if ((a[i] - a[j]) % (i - j) == 0) {
                int x = (a[i] - a[j]) / (i - j);
                if (x <= sqrtmaxx) continue;
                f[i][x] = max(f[i][x], f[j][x] + 1);
                ans = max(f[i][x] + 1, ans);
            }
        }
    }

    for (int i = 1; i <= n; i++) f[i].clear();    // 清空数组

    return ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], maxx = max(maxx, a[i]);
    sqrtmaxx = sqrt(maxx);

    int ans1 = 0, ans2 = 0;
    ans1 = max_keep();
    reverse(a + 1, a + n + 1);                       // 应对公差为负数的情况
    ans2 = max_keep();

    cout << n - max(ans1, ans2) << '\n';
    return 0;
}