2021-03-22：小虎去买苹果，商店只提供两种类型的塑料袋，每种类型都有任意数量。1.能装下6个苹果的袋子，2.能装下8个苹果的袋子。小虎可以自由使用两种袋子来装苹果，但是小虎有强迫症，他要求自己使用的袋子数量必须最少，且使用的每个袋子必须装满。给定一个正整数N，返回至少使用多少袋子。如果N无法让使用的每个袋子必须装满，返回-1。

2021-03-22：小虎去买苹果，商店只提供两种类型的塑料袋，每种类型都有任意数量。1.能装下6个苹果的袋子，2.能装下8个苹果的袋子。小虎可以自由使用两种袋子来装苹果，但是小虎有强迫症，他要求自己使用的袋子数量必须最少，且使用的每个袋子必须装满。给定一个正整数N，返回至少使用多少袋子。如果N无法让使用的每个袋子必须装满，返回-1。

福大大 答案2021-03-22：

1.自然智慧即可。

N一定是2的倍数，否则两种袋子始终装不满，原因是6和8的最小公倍数是2。

先全部装8号袋，剩下的苹果装6号袋，6号不满，一个8号袋的苹果倒入6号袋，直到6号袋能装满为止。

2.根据结果反推，找规律。

N一定是2的倍数，否则两种袋子始终装不满，原因是6和8的最小公倍数是2。

N大于等于18时，从18开始，8个数字一组。

N小于18时，直接给出结果。

代码用golang编写，代码如下：

package main

import "fmt"

func main() {
    for apple := 100; apple <= 120; apple++ {
        fmt.Println(apple, " : ", minBages1(apple), " : ", minBages2(apple))
    }
}
func minBages1(apple int) int {
    if apple < 0 {
        return -1
    }
    bag8 := apple / 8
    rest := apple - bag8*8
    for bag8 >= 0 {
        // rest 个
        if rest%6 == 0 {
            return bag8 + (rest / 6)
        } else {
            bag8--
            rest += 8
        }
    }
    return -1
}
func minBages2(apple int) int {
    if (apple & 1) != 0 { // 如果是奇数，返回-1
        return -1
    }
    if apple < 18 {
        if apple == 0 {
            return 0
        }
        if apple == 6 || apple == 8 {
            return 1
        }
        if apple == 12 || apple == 14 || apple == 16 {
            return 2
        }
        return -1
    }
    return (apple-18)/8 + 3
}

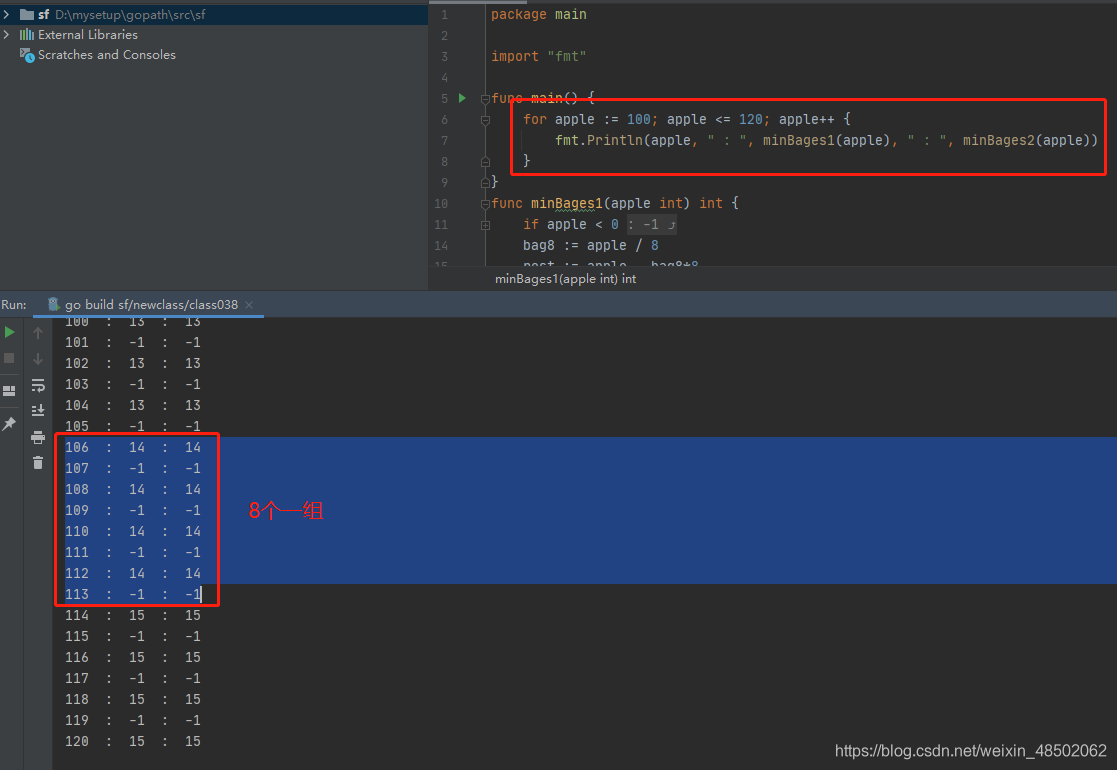
执行结果如下：

---

左神java代码

评论