[POC]

1. 奇异值分解的本质

特征值分解只能够对于方阵提取重要特征，

Ax=λx λ为特征值 x为对应的特征向量

奇异值分解可以对于任意矩阵；



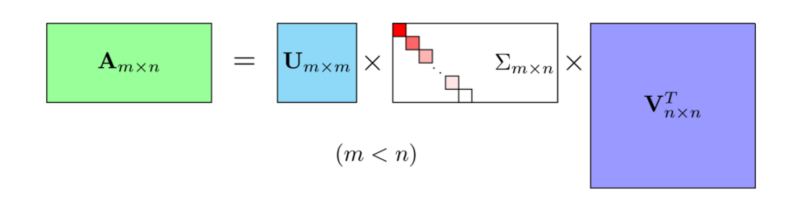
注意看中间的矩阵是一个对角矩阵，颜色越深越起作用-值越大 颜色越浅越接近0

U是左奇异矩阵，V是右奇异矩阵，均是正交矩阵，

中间的Σ是对角阵，除对角线元素外都是0，对角线元素是奇异值。

在大多数情况下，前10%甚至前1%的奇异值的和便占据了全部奇异值之和的99%以上了，因此当利用奇异值分解对数据进行压缩时，我们可以用前 个大的奇异值来近似描述矩阵。

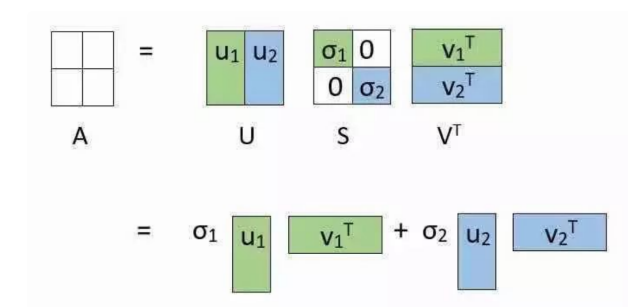
其他性质：



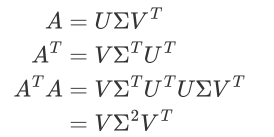
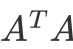
  1. 特征向量张成的矩阵就是SVD中的v矩阵
  2. 协方差矩阵的特征值矩阵等于奇异值矩阵的平方

用处呢？

降维 n维降到k维：

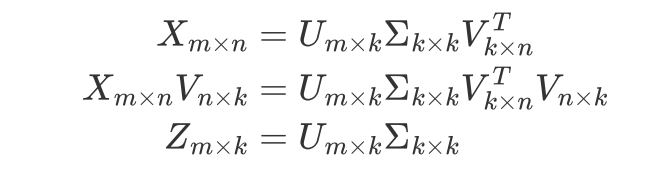
数据压缩 m行降到k行：

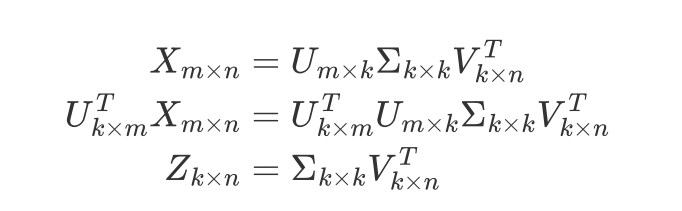
机器学习-无监督机器学习-SVD奇异值分解-24的更多相关文章

  1. 机器学习（十七）— SVD奇异值分解

    奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域.是 ...

  2. 学习笔记CB008:词义消歧、有监督、无监督、语义角色标注、信息检索、TF-IDF、隐含语义索引模型

    词义消歧,句子.篇章语义理解基础,必须解决.语言都有大量多种含义词汇.词义消歧,可通过机器学习方法解决.词义消歧有监督机器学习分类算法,判断词义所属分类.词义消歧无监督机器学习聚类算法,把词义聚成多类 ...

  3. 深度学习——无监督，自动编码器——尽管自动编码器与 PCA 很相似，but自动编码器既能表征线性变换，也能表征非线性变换；而 PCA 只能执行线性变换

    自动编码器是一种有三层的神经网络:输入层.隐藏层(编码层)和解码层.该网络的目的是重构其输入,使其隐藏层学习到该输入的良好表征. 自动编码器神经网络是一种无监督机器学习算法,其应用了反向传播,可将目标 ...

  4. 1(1).有监督 VS 无监督

    对比一 : 有标签 vs 无标签 有监督机器学习又被称为“有老师的学习”,所谓的老师就是标签.有监督的过程为先通过已知的训练样本(如已知输入和对应的输出)来训练,从而得到一个最优模型,再将这个模型应用 ...

  5. [机器学习]-SVD奇异值分解的基本原理和运用

    SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...

  6. darktrace 亮点是使用的无监督学习（贝叶斯网络、聚类、递归贝叶斯估计）发现未知威胁——使用无人监督 机器学习反而允许系统发现罕见的和以前看不见的威胁，这些威胁本身并不依赖 不完善的训练数据集。 学习正常数据，发现异常！

    先说说他们的产品:企业免疫系统(基于异常发现来识别威胁) 可以看到是面向企业内部安全的! 优点整个网络拓扑的三维可视化企业威胁级别的实时全局概述智能地聚类异常泛频谱观测 - 高阶网络拓扑;特定群集,子 ...

  7. 简单易学的机器学习算法—SVD奇异值分解

    简单易学的机器学习算法-SVD奇异值分解 一.SVD奇异值分解的定义     假设M是一个的矩阵,如果存在一个分解: 其中的酉矩阵,的半正定对角矩阵,的共轭转置矩阵,且为的酉矩阵.这样的分解称为M的奇 ...

  8. 【机器学习】Google机器学习工程的43条最佳实践

    https://blog.csdn.net/ChenVast/article/details/81449509 本文档旨在帮助那些掌握机器学习基础知识的人从Google机器学习的最佳实践中获益.它提供 ...

  9. kaggle信用卡欺诈看异常检测算法——无监督的方法包括： 基于统计的技术，如BACON *离群检测 多变量异常值检测 基于聚类的技术；监督方法： 神经网络 SVM 逻辑回归

    使用google翻译自:https://software.seek.intel.com/dealing-with-outliers 数据分析中的一项具有挑战性但非常重要的任务是处理异常值.我们通常将异 ...

  10. SVD奇异值分解的基本原理和运用

    SVD奇异值分解: SVD是一种可靠的正交矩阵分解法.可以把A矩阵分解成U,∑,VT三个矩阵相乘的形式.(Svd(A)=[U*∑*VT],A不必是方阵,U,VT必定是正交阵,S是对角阵<以奇异值 ...

随机推荐

  1. 自上而下的LL(1)语法分析法

    LL(1)文法:从文法的开始符,向下推导,推出句子. 对文法G的句子进行确定的自顶向下语法分析的充分必要条件是,G的任意两个具有相同左部的 产生式A->α|β 满足下列条件: (1)如果α.β均 ...

  2. 华企盾DSC半透明无法打开加密文件常见处理方法

    1.查看客户端日志进程是否显示legal:1 2.半透明只支持双击打开 3.半透明进程不能设置HOOK白名单 4.检查调用的进程是否都加了 5.半透明程序的运行方式不可以以管理员启动,去掉" ...

  3. Python——第五章：处理异常try、except、else、finally

    处理异常try 和 except 在 Python 中,try 和 except 语句用于处理异常(错误).通过使用这两个关键字,你可以编写代码来捕获和处理可能发生的异常,以保持程序的稳定性. try ...

  4. C++ Qt开发：Charts与数据库组件联动

    Qt 是一个跨平台C++图形界面开发库,利用Qt可以快速开发跨平台窗体应用程序,在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置,实现图形化开发极大的方便了开发效率,本章将重点介绍Charts组 ...

  5. Python汉诺塔递归算法实现

    关于用递归实现的原理,请查看我之前的文章: C语言与汉诺塔 C#与汉诺塔 以下为代码: count = 0 def move(pile, src, tmp, dst): global count if ...

  6. JPA object references an unsaved transient instance - save the transient instance before flushing

    nested exception is org.springframework.dao.InvalidDataAccessApiUsageException: org.hibernate.Transi ...

  7. 人大金仓驱动包kingbasejdbc8.6.0.jar V8驱动jar包

    人大金仓驱动包kingbasejdbc8.6.0.jar V8驱动jar包 工作上要将kingbaseV8数据库整合到项目,我在官网找了半天,连个jdbc驱动包下载入口都找不到,简直就是官方文档毫无诚 ...

  8. Java异常处理之数字溢出问题

    在进行 Java 开发时,经常会遇到数字溢出的问题.这个问题在很多程序中都非常常见,尤其是在进行数值计算的时候.Java 中提供了一种异常机制来处理这种情况,我们可以在代码中使用 try-catch ...

  9. 容器中域名解析流程以及不同dnsPolicy对域名解析影响

    本文分享自华为云社区<容器中域名解析流程以及不同dnsPolicy对域名解析影响>,作者:可以交个朋友 . 一.coreDNS背景 部署在kubernetes集群中的容器业务通过coreD ...

  10. 三问三答：细数GaussDB迁移的核心技术

    摘要:本文从客户视角的三个疑问出发,一起了解华为云GaussDB数据库的迁移解决方案具有哪些核心技术,如何做到让客户迁移过程安心.放心.省心. 迁移是数据库选型过程中客户最为关心的话题之一,经过大量的 ...