力扣304(java)-二维区域和检索-矩阵不可变（中等）

题目：

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。
实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和

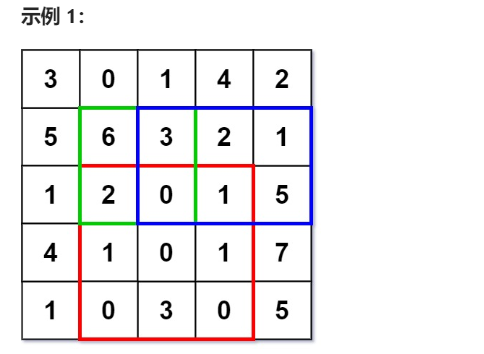
输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-105 <= matrix[i][j] <= 105
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 104 次 sumRegion 方法

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/range-sum-query-2d-immutable
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

1.先求presum[i][j]:从[0][0]到[i][j]位置的子矩阵所有元素之和；

2.再利用presum求子矩阵的面积。

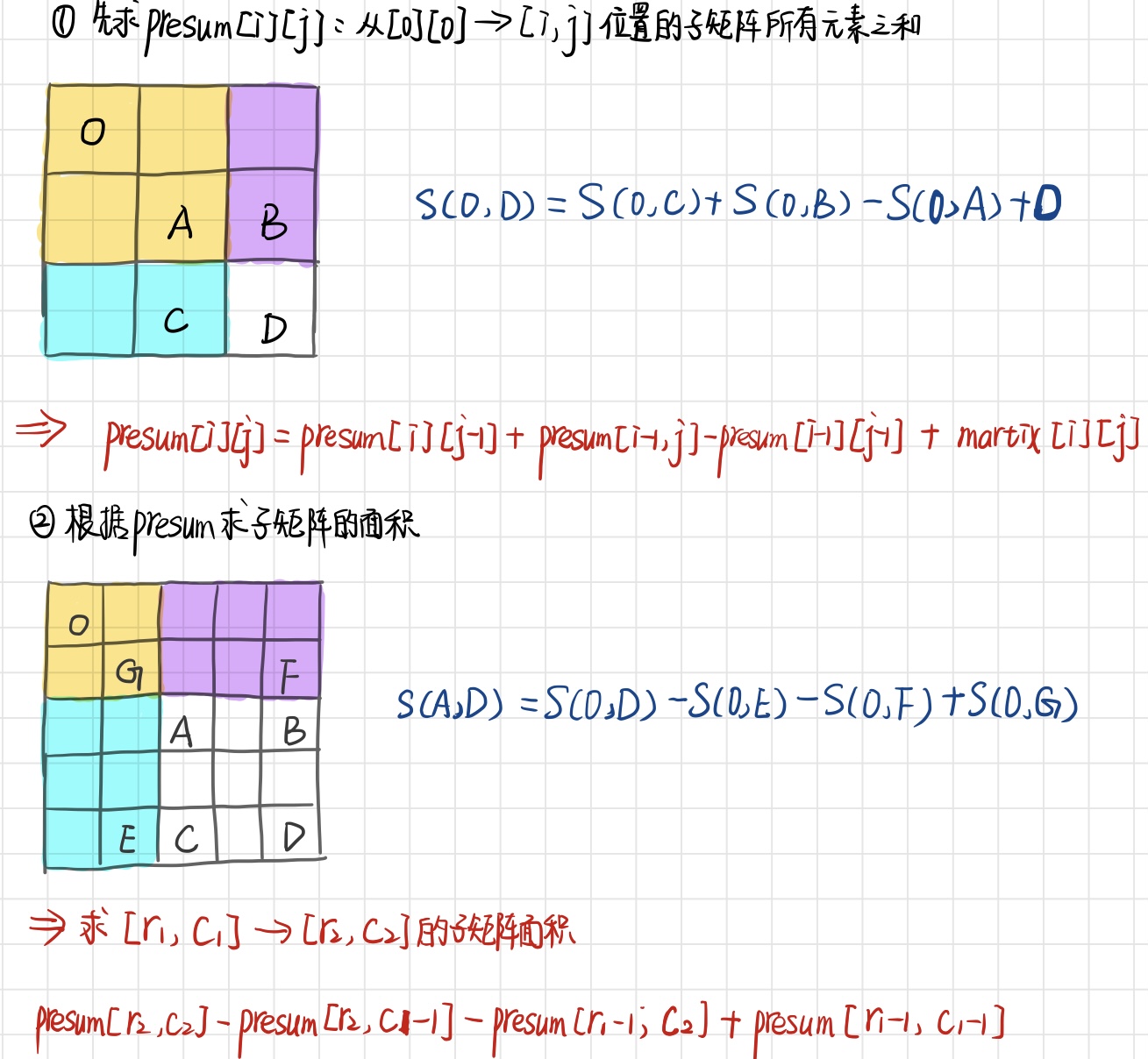
 代码：

注意： presum 矩阵要比原矩阵多一行一列，是为了让第 0 行与第 0 列的元素也能使用上面的递推公式。如果 preSum 矩阵大小和 martix 大小相等，则需要对第 0 行与第 0 列特殊判断。所以求前缀和时从 1 开始，类似于一维前缀和，也是在比原数组多一个元素，主要是为了 presum[0] 时也能直接表示，不然需要特殊判断。

 1 class NumMatrix {
 2     int[][] presum;
 3
 4     public NumMatrix(int[][] matrix) {
 5             presum = new int[matrix.length + 1][matrix[0].length + 1];
 6             for(int i = 0; i < matrix.length; i++){
 7                 for(int j = 0; j < matrix[0].length; j++){
 8                     presum[i + 1][j + 1] = presum[i + 1][j] + presum[i][j + 1] - presum[i][j] + matrix[i][j];
 9                 }
10             }
11     }
12     public int sumRegion(int row1, int col1, int row2, int col2) {
13         return presum[row2 + 1][col2 + 1] - presum[row2 + 1][col1] -presum[row1][col2 + 1] + presum[row1][col1];
14     }
15 }
16
17 /**
18  * Your NumMatrix object will be instantiated and called as such:
19  * NumMatrix obj = new NumMatrix(matrix);
20  * int param_1 = obj.sumRegion(row1,col1,row2,col2);
21  */