一次考试的dp题

很明显是dp

看题目的时候我们先进行初步的思考，发现一个性质

一个点时不可能被重复覆盖三次的
很显然，如果一个点被覆盖了3次，这3个覆盖他的区间一定是有一个区间被完全包含的，因为有贡献的左右端点只有两个

这种dp一看就是要按照右端点排序，不然会有严重的后效性无法处理
排完序后还是有后效性，第一维的状态已经很明显了，是选到了第i个区间
看完题解后发现为了后效性的处理第二维一定是和所选区间的最后的元素有关系的
这里就设第二维为区间 [j,r_i] 被覆盖了一次(只能是一次 )

这样就考虑到了这个需要决策的选择的影响处理

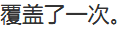
这就是最后的dp状态

关于转移

有两种情况，一个是这个区间刚刚卡好，那就之间在这个里面转移，即：

另外一种，r[j]卡在了这个区间的里面，即：

然后就没了

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read()
{
    char c=getchar();int a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
const int N=4001;
int f[N][N],awa[N][N],T,n,m,ans=1<<30;
struct qwq{int l,r,v;}a[N];
bool mmp(qwq a,qwq b)
{
    return a.r<b.r;
}
int main()
{
    freopen("intervals.in","r",stdin);
    freopen("intervals.out","w",stdout);
    T=read();
    while(T--)
    {
        ans=(1<<30);
        n=read();m=read();
        for(int i=1;i<=n;i++)
        {
            a[i].l=read();
            a[i].r=read();
            a[i].v=read();
        }
        sort(a+1,a+n+1,mmp);
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                f[i][j]=awa[i][j]=(1<<30);
            }
        }
        for(int i=1;i<=n;i++)
        {
            if(a[i].l==1)
            {
                for(int j=1;j<=a[i].r;j++)
                {
                    awa[i][j]=f[i][j]=a[i].v;
                }
            }
            for(int j=1;j<i;j++)
            {
                if(a[j].r+1==a[i].l)
                {
                    f[i][a[i].l]=min(f[i][a[i].l],max(awa[j][a[j].r],a[i].v));
                }
                if(a[i].l<=a[j].r&&a[j].r<=a[i].r)
                {
                    f[i][a[j].r+1]=min(f[i][a[j].r+1],max(awa[j][a[i].l],a[i].v+a[j].v));
                }
            }
            awa[i][1]=min(awa[i][1],f[i][1]);
            for(int j=2;j<=a[i].r;j++)
            {
                awa[i][j]=min(awa[i][j],min(awa[i][j-1],f[i][j]));
            }
            if(a[i].r==m)ans=min(ans,awa[i][a[i].r]);
        }
        if(ans==(1<<30))ans=-1;
        printf("%d\n",ans);
    }