linux下磁盘分区详解

Centos下磁盘管理

    1.磁盘分区格式说明

linux分区不同于windows，linux下硬盘设备名为（IDE硬盘为hdx（x为从a—d）因为IDE硬盘最多四个，SCSI，SATA，USB硬盘为sdx（x为a—z）），硬盘主分区最多为4个，不用说大家也知道…..所以主分区从sdb1开始到sdb4，逻辑分区从sdb5开始，（逻辑分区永远从sdb5开始…）设备名可以使用fdisk –l查看

2.分区详解

使用ssh远程连接工具登录到系统，使用fdisk -l命令查看磁盘状态

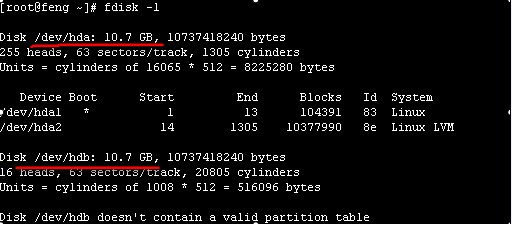
此处可以看到两块硬盘hda和hdb，第一块硬盘hda是装好系统的。hdb硬盘是未进行分区的。

本例将这个10G的硬盘分区，分区计划：分一个主分区 ，大小3G，文件格式ext3.三个逻辑分区，大小分别为2G，2G，3G。实际分区个数和大小可论情况所定。

下面就是分区的详细步骤，由于是每一步都进行了截图和说明，内容略显复杂，其实很简单。

输入 fdisk /dev/hdb 然后回车，给硬盘进行分区。如下图

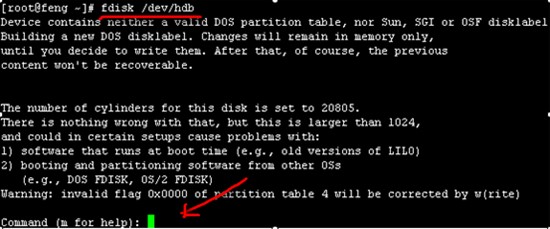
输入n回车新建分区，接着再输入p回车新建主分区，如图

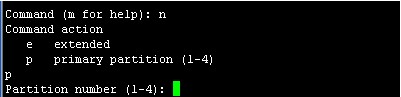
此处要求选择分区号在1-4间，输入1回车

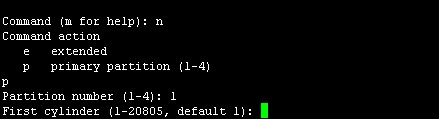
First cylinder (1-20805, default 1):这里是设置分区起始的柱面，直接回车选择默认即可，回车后如下图

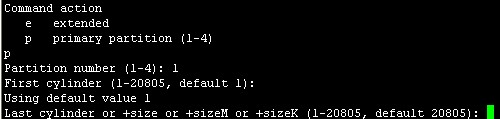
Last cylinder or +size or +sizeM or +sizeK (1-20805, default 20805):此处是设置分区结束柱面，+3G表示从起始柱面开始向后3G结束，也是是设置分区大小为3G，输入+3G后回车，如下图所示

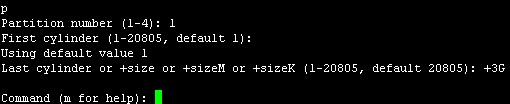
此处可输入p查看分区是否成功，输入p回车，如下图：显示分区成功

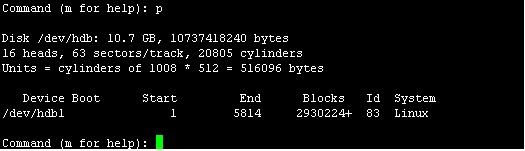
接下来我们就划分扩展分区，按n回车

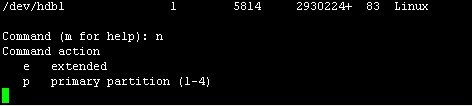
这里输入e，表示创建扩展分区，输入e回车

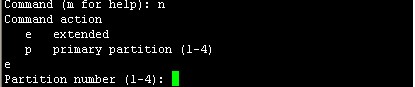
输入分区号2回车

此处直接按回车键，表示选择默认

此处也是直接回车选择默认，表示将划分第一个主分区后的磁盘全部划分个这个逻辑分区

此处可在此输入命令p查看当前分区状态，如下图

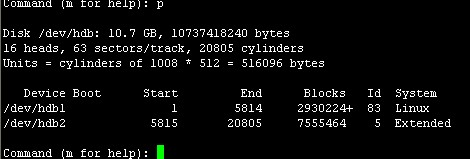
此处就开始划分扩展分区hdb2下的逻辑分区吧！接着上图，输入命令n回车

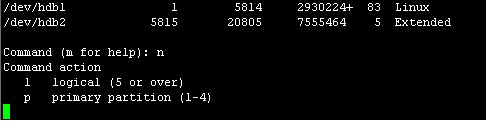
此处输入l表示选择创建逻辑分区，输入l回车

此处直接使用回车，表示选择默认

此处输入+2G，表示划分分区大小为2G，输入+2G回车

此处要按计划再划分出两个逻辑空间，输入n回车，然后输入l回车选择逻辑分区，然后直接回车选择默认起始柱面，输入+2G回车设置分区大小

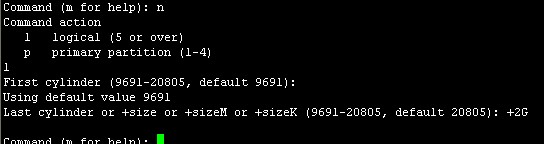
下面就要将扩展分区的磁盘大小全部分给最后一个逻辑分区，输入n回车，然后输入l选择逻辑分区，然后直接回车选择默认起始柱面，最后不设置磁盘大小直接回车

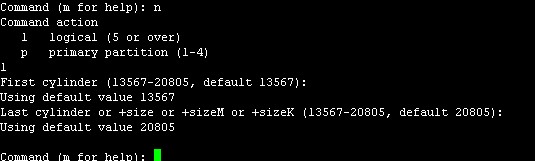
再次输入p查看当前分区状态

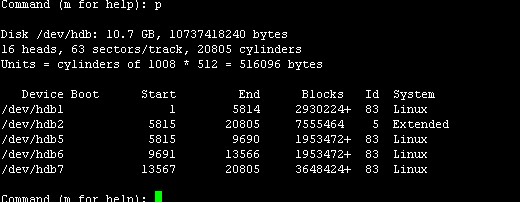
划分的空间与我们计划划分相同，最后输入w回车，进行保存退出。

再次使用fdisk -l命令就可以查看到磁盘hdb已经分区成功。

磁盘划分成功，下面就要对分区进行格式化了

使用命令 mkfs -t ext3  /dev/hdb1

mkfs -t ext3  /dev/hdb5

mkfs -t ext3  /dev/hdb6

mkfs -t ext3  /dev/hdb7

分别对磁盘进行格式化处理，格式化为ext3文件类型

自此分区流程算是完成啦！

附：fdisk和mkfs，mkswap命令的参数解释

fdisk命令详解：

m：获取帮助

n：新建分区

p：显示分区表

d：删除分区

b：设置卷标

w：写入分区表

t：改变分区文件系统类型

v：检验分区

l：显示fdisk所支持的文件系统代码

q：退出

文件系统的建立：

mkfs参数分区

-t文件系统类型指定建立的文件系统类型

注：mkfs -t ext3 =mkfs.ext3

-c建立文件系统之前检查有无坏道

-l文件名：从文件中读取坏道的情况

-v显示详细情况

mkswap 分区在分区上建立交换分区

例：在hdb7上建立交换分区命令如下：

mkswap/etc/hdb7