POJ 3744 Scout YYF I（矩阵快速幂优化+概率dp）

http://poj.org/problem?id=3744

题意：

现在有个屌丝要穿越一个雷区，雷分布在一条直线上，但是分布的范围很大，现在这个屌丝从1出发，p的概率往前走1步，1-p的概率往前走2步，求最后顺利通过雷区的概率。

思路：

首先很容易能得到一个递推式：$dp[i]=p*dp[i-1]+(1-p)*dp[i-2]$。但是直接递推肯定不行，然后我们发现这个很容易构造出矩阵来，但是这样还是太慢。

接下来讲一下如何优化，对于第i个雷，它的坐标为x[i]，那么那顺利通过它的话，只能在x[i]-1的位置走2步。

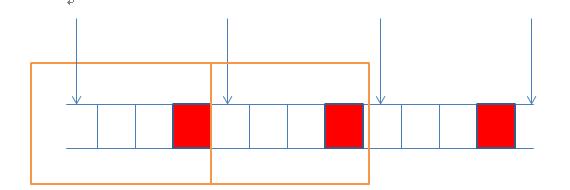
观察上图，可以发现每次起点就相当于是雷后面的一个格子，这样的话我们就可以分块处理（有多少雷就分多少块），先计算出起点到雷的概率y，那么1-y就是顺利通过这块的概率。最后乘法原理乘起来即可。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n;
 double p, ans;
 int x[];

 struct Matrix
 {
     double mat[][];
     Matrix()
     {
         for(int i=;i<;i++)
         for(int j=;j<;j++)
             mat[i][j]=;
     }
     Matrix operator* (const Matrix& b) const
     {
         Matrix c;
         for(int i=;i<;i++)
         for(int j=;j<;j++)
         for(int k=;k<;k++)
             c.mat[i][j]+=mat[i][k]*b.mat[k][j];
         return c;
     }
 }base;

 Matrix q_pow(Matrix base, int n)
 {
     Matrix res;
     res.mat[][]=res.mat[][]=;
     while(n)
     {
         if(n&) res=res*base;
         base=base*base;
         n>>=;
     }
     return res;
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%lf",&n,&p))
     {
         for(int i=;i<=n;i++)  scanf("%d",&x[i]);
         sort(x+,x+n+);
         base.mat[][]=p;
         base.mat[][]=-p;
         base.mat[][]=;
         base.mat[][]=;
         ans=;
         Matrix tmp=q_pow(base, x[]-);
         ans*=(-tmp.mat[][]);
         for(int i=;i<=n;i++)
         {
             if(x[i]==x[i-])  continue;
             tmp=q_pow(base, x[i]-x[i-]-);
             ans*=(-tmp.mat[][]);
         }
         printf("%.7f\n",ans);
     }
     return ;
 }