图像处理gamma修正（伽马γ校正）的原理和实现算法

☞ ░ 前往老猿Python博文目录 ░

本文转自博客园：淇淇宝贝的文章《图像处理之gamma校正》，原文链接：https://www.cnblogs.com/qiqibaby/p/5325193.html

一、gamma校正背景

在电视和图形监视器中，显像管发生的电子束及其生成的图像亮度并不是随显像管的输入电压线性变化，电子流与输入电压相比是按照指数曲线变化的，输入电压的指数要大于电子束的指数。这说明暗区的信号要比实际情况更暗，而亮区要比实际情况更高。所以，要重现摄像机拍摄的画面，电视和监视器必须进行伽玛补偿。这种伽玛校正也可以由摄像机完成。我们对整个电视系统进行伽玛补偿的目的，是使摄像机根据入射光亮度与显像管的亮度对称而产生的输出信号，所以应对图像信号引入一个相反的非线性失真，即与电视系统的伽玛曲线对应的摄像机伽玛曲线，它的值应为1/γ，我们称为摄像机的伽玛值。电视系统的伽玛值约为2.2，所以电视系统的摄像机非线性补偿伽玛值为0.45。彩色显像管的伽玛值为2.8，它的图像信号校正指数应为1/2.8=0.35，但由于显像管内外杂散光的影响，重现图像的对比度和饱和度均有所降低，所以彩色摄像机的伽玛值仍多采用0.45。在实际应用中，我们可以根据实际情况在一定范围内调整伽玛值，以获得最佳效果。

　

二、gamma校正定义

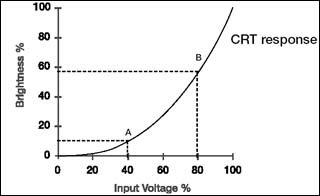
(Gamma Correction，伽玛校正）：所谓伽玛校正就是对图像的伽玛曲线进行编辑，以对图像进行非线性色调编辑的方法，检出图像信号中的深色部分和浅色部分，并使两者比例增大，从而提高图像对比度效果。计算机绘图领域惯以此屏幕输出电压与对应亮度的转换关系曲线，称为伽玛曲线（Gamma Curve）。

以传统CRT（Cathode Ray Tube）屏幕的特性而言，该曲线通常是一个乘幂函数，Y=(X+e)γ，其中，Y为亮度、X为输出电压、e为补偿系数、乘幂值（γ）为伽玛值，改变乘幂 值（γ）的大小，就能改变CRT的伽玛曲线。典型的Gamma值是0.45，它会使CRT的影像亮度呈现线性。使用CRT的电视机等显示器屏幕，由于对于 输入信号的发光灰度，不是线性函数，而是指数函数，因此必需校正。

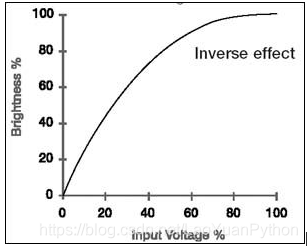
三、 gamma校正原理

假设图像中有一个像素，值是 200 ，那么对这个像素进行校正必须执行如下步骤：

1. 归一化 ：将像素值转换为 0 ～ 1 之间的实数。 算法如下 : ( i + 0. 5)/256 这里包含 1 个除法和 1 个加法操作。对于像素 A 而言 , 其对应的归一化值为 0. 783203 。

2. 预补偿 ：根据公式 , 求出像素归一化后的 数据以 1 /gamma 为指数的对应值。这一步包含一个 求指数运算。若 gamma 值为 2. 2 , 则 1 /gamma 为 0. 454545 , 对归一化后的 A 值进行预补偿的结果就 是 0. 783203 ^0. 454545 = 0. 894872 。

3. 反归一化 ：将经过预补偿的实数值反变换为 0 ～ 255 之间的整数值。具体算法为 : f*256 - 0. 5 此步骤包含一个乘法和一个减法运算。续前 例 , 将 A 的预补偿结果 0. 894872 代入上式 , 得到 A 预补偿后对应的像素值为 228 , 这个 228 就是最后送 入显示器的数据。

如上所述如果直接按公式编程的话，假设图像的分辨率为 800*600 ，对它进行 gamma 校正，需要执行 48 万个浮点数乘法、除法和指数运算。效率太低，根本达不到实时的效果。

针对上述情况，提出了一种快速算法，如果能够确知图像的像素取值范围 , 例如 , 0 ～ 255 之间的整数 , 则图像中任何一个像素值只能 是 0 到 255 这 256 个整数中的某一个 ; 在 gamma 值 已知的情况下 ,0 ～ 255 之间的任一整数 , 经过“归一 化、预补偿、反归一化”操作后 , 所对应的结果是唯一的 , 并且也落在 0 ～ 255 这个范围内。

如前例 , 已知 gamma 值为 2. 2 , 像素 A 的原始值是 200 , 就可求得 经 gamma 校正后 A 对应的预补偿值为 228 。基于上述原理 , 我们只需为 0 ～ 255 之间的每个整数执行一次预补偿操作 , 将其对应的预补偿值存入一个预先建立的 gamma 校正查找表 (LUT:Look Up Table) , 就可以使用该表对任何像素值在 0 ～ 255 之 间的图像进行 gamma 校正。

关于moviepy的介绍请参考《PyQt+moviepy音视频剪辑实战文章目录》或《moviepy音视频开发专栏》。

关于收费专栏

老猿的付费专栏《使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程，付费专栏《moviepy音视频开发专栏》详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理，两个专栏加起来只需要19.9元，都适合有一定Python基础但无相关专利知识的小白读者学习。这2个收费专栏都有对应免费专栏，只是收费专栏的文章介绍更具体、内容更深入、案例更多。

对于缺乏Python基础的同仁，可以通过老猿的免费专栏《专栏：Python基础教程目录》从零开始学习Python。

如果有兴趣也愿意支持老猿的读者，欢迎购买付费专栏。

跟老猿学Python、学5G!

☞ ░ 前往老猿Python博文目录 ░