Java数据结构——二叉搜索树

定义
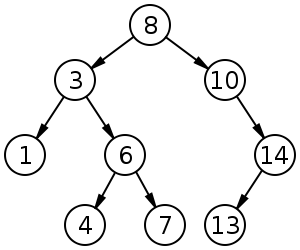
二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

性质
1，任意节点x，其左子树中的key不大于x.key，其右子树中的key不小于x.key。
2，不同的二叉搜索树可以代表同一组值的集合。
3，二叉搜索树的基本操作和树的高度成正比，所以如果是一棵完全二叉树的话最坏运行时间为Θ(lgn)，但是若是一个n个节点连接成的线性树，那么最坏运行时间是Θ(n)。
4，根节点是唯一一个parent指针指向NIL节点的节点。
5，每一个节点至少包括key、left、right与parent四个属性，构建二叉搜索树时，必须存在针对key的比较算法。

简单实现（curd操作）

TreeNode.java

public class TreeNode {
private int data;
private TreeNode leftChild;
private TreeNode rightChild;
public TreeNode parent;

public int getData() {
return data;
}

public void setData(int data) {
this.data = data;
}

public TreeNode getLeftChild() {
return leftChild;
}

public void setLeftChild(TreeNode leftChild) {
this.leftChild = leftChild;
}

public TreeNode getRightChild() {
return rightChild;
}

public void setRightChild(TreeNode rightChild) {
this.rightChild = rightChild;
}

public TreeNode getParent() {
return parent;
}

public void setParent(TreeNode parent) {
this.parent = parent;
}

public TreeNode(int data) {
super();
this.data = data;
}

}

BinarySearchTree.java（不含main类，可以自己写main类）

public class BinarySearchTree {
private TreeNode root;

//构造二叉搜索树
public TreeNode creatSearchBinaryTree(int data) {
TreeNode node = null;
TreeNode parent = null;
if (root == null) {
node = new TreeNode(data);
root = node;
}
node = root;
while (node != null) {
parent = node;
if (data > node.data) {
node = node.rightChild;
} else if (data < node.data) {
node = node.leftChild;
} else {
return node;
}
}
node = new TreeNode(data);
if (data < parent.data) {
parent.leftChild = node;
} else {
parent.rightChild = node;
}
node.parent = parent;
return node;
}

//中序遍历
public void inOrder(TreeNode n) {
if (n != null) {
inOrder(n.getLeftChild());
System.out.print(n.data + " ");
inOrder(n.getRightChild());
}
}

// 添加节点
public boolean insertNode(int data) {
TreeNode node = new TreeNode(data);
if (root == null) {
root = node;
return true;
}
TreeNode parent = root;
TreeNode current = root;
while (true) {
parent = current;
if (data == current.data) {
return true;
}
if (data < current.data) {
current = current.leftChild;
if (current == null) {
parent.leftChild = node;
return true;
}
} else {
current = current.rightChild;
if (current == null) {
parent.rightChild = node;
return true;
}
}
}

}

// 删除节点
public boolean deleteNode(int data) {
TreeNode current = root;
TreeNode parent = root;
boolean isLeftChild = true;
// 找到要删除的点，并记录该节点是否为左节点
while (current.data != data) {
parent = current;
if (data < current.data) {
isLeftChild = true;
current = current.leftChild;
} else {
isLeftChild = false;
current = current.rightChild;
}
if (current == null) {
return false;
}
}
// 如果删除节点为子节点
if (current.leftChild == null && current.rightChild == null) {
if (current == root) {
root = null;
} else {
if (isLeftChild == true) {
parent.leftChild = null;
} else {
parent.rightChild = null;
}
}
// 如果删除节点只有一个子节点
} else if ((current.leftChild != null && current.rightChild == null)
|| (current.leftChild == null && current.rightChild != null)) {
if (current.rightChild == null) {
if (root == current) {
root = current.leftChild;
} else {
if (isLeftChild == true) {
parent.leftChild = current.leftChild;
} else {
parent.rightChild = current.leftChild;
}
}
} else {
if (root == current) {
root = current.rightChild;
} else {
if (isLeftChild == true) {
parent.leftChild = current.rightChild;
} else {
parent.rightChild = current.rightChild;
}
}
}
// 如果删除节点同时有左右节点,找后继节点
} else if (current.leftChild != null && current.rightChild != null) {
TreeNode processer = processer(current);
if (current == root) {
root = processer;
} else {
if (isLeftChild == true) {
parent.leftChild = processer;
} else {
parent.rightChild = processer;
}
}
processer.leftChild = current.leftChild;
}
return true;
}

//寻找后继节点
private TreeNode processer(TreeNode delNode) {
TreeNode parent = delNode;
TreeNode success = delNode;
TreeNode current = delNode.rightChild;
while (current != null) {
parent = current;
success = current;
current = current.leftChild;
}
if (success != delNode.rightChild) {
parent.leftChild = success.rightChild;
success.rightChild = delNode.rightChild;
}
return success;
}

// 修改节点
public boolean updateNode(int oldData, int newData) {
boolean del = deleteNode(oldData);
insertNode(newData);
if (del == true) {
return true;
} else {
return false;
}
}

// 查找节点
public TreeNode findNode(int data) {
TreeNode current = root;
while (current.data != data) {
if (data < current.data) {
current = current.leftChild;
} else {
current = current.rightChild;
}
if (current == null) {
return null;
}
}
return current;
}
}