笔记 | 第一个量子算法：Deutsch-Jozsa算法，非常好懂！

《关于胡小兔的博客又诈尸了这件事》

信息物理真是难啊！上节课讲了量子计算的最基础的概念和Deutsch-Jozsa算法，我看了好几天才看懂……

等考完试估计我就忘了，所以今天先写个博客给未来的我讲讲！

前置技能

// 这部分暂时鸽了。

// 信女愿在博客更新量子计算基础合集，只求小学期两门A-……

// 不过安利一个网站：IBM的量子计算教程，还可以用IBM的qiskit库实践！而且这个网站的颜值真的很高2333

Deutsch算法

众所周知，量子计算机可以利用量子比特（qubit）的叠加态，实现并行计算，从而快速计算一些传统计算机上复杂度很高的问题。但是这种并行计算是怎么实现的呢……？为了理解量子并行，我们找到了一个很好的例子——Deutsch算法。顾名思义，学会这个Deutsch算法，你的Deutsch-Jozsa就学会一大半了（雾

目标

有一个未知的黑盒\(f: \{0, 1\} \rightarrow \{0, 1\}\)，求\(f(0) \oplus f(1)\)（\(\oplus\)表示异或）。

传统算法

在传统计算机上，我们必须调用\(f\)函数两次，一次求\(f(0)\)，一次求\(f(1)\)，再异或起来，得到答案。但是在量子电路中，只需要一次计算！

量子算法

Deutsch算法就是如下的电路：

其中，中间那个大方块\(U_f\)是一个特殊的门，输入\(x\)和\(y\)，输出\(x\)和\(y\oplus f(x)\)。三个\(H\)门是Hadamard门，要记得：

\[H|0\rangle = |+\rangle = (|0\rangle + |1\rangle)/\sqrt2
\]

\[H|1\rangle = |-\rangle = (|0\rangle - |1\rangle)/\sqrt2
\]

\[H|+\rangle = |0\rangle
\]

\[H|-\rangle = |1\rangle
\]

电路的输入是固定的：\(H|\psi_0\rangle = |01\rangle\)。接下来，我们来算一下\(|\psi_1\rangle, |\psi_2\rangle, |\psi_3\rangle\)都是什么，然后就知道测量结果和\(f\)的关系了！

刚刚说过，\(H|0\rangle = |+\rangle = (|0\rangle + |1\rangle)/\sqrt2, H|1\rangle = |-\rangle = (|0\rangle - |1\rangle)/\sqrt2\)，所以

\[|\psi_1\rangle = (H|0\rangle)(H|1\rangle) = (|0\rangle + |1\rangle)(|0\rangle - |1\rangle)/2.
\]

接下来就要考虑这个\(U_f\)了。为了计算方便，我们先设它第一个输入值是\(|x\rangle\)，第二个输入值直接代入\((|0\rangle - |1\rangle)/\sqrt2\)。那么，

\[\begin{aligned}
U_f |x\rangle (|0\rangle - |1\rangle)/\sqrt2 &= |x\rangle (|f(x)\rangle - |1\oplus f(x)\rangle)/\sqrt2 \\
&= \begin{cases}
|x\rangle (|0\rangle - |1\rangle)/\sqrt2, \text{ if }f(x) = 0, \\
|x\rangle (|1\rangle - |0\rangle)/\sqrt2, \text{ if }f(x) = 1 \\
\end{cases}\\
&= (-1)^{f(x)} |x\rangle (|0\rangle - |1\rangle)/\sqrt2.
\end{aligned}\]

看起来非常的简洁！

接下来把\(x = (|0\rangle + |1\rangle) / \sqrt2\)代进去：

\[\begin{aligned}
|\psi_2\rangle &= U_f (|0\rangle + |1\rangle)(|0\rangle - |1\rangle)/2 \\
&= \left[(-1)^{f(0)} |0\rangle + (-1)^{f(1)} |1\rangle\right] (|0\rangle - |1\rangle)/2 \\
&= (-1)^{f(0)} \left[|0\rangle + (-1)^{f(0)\oplus f(1)} |1\rangle\right] (|0\rangle - |1\rangle)/2. \\
\end{aligned}\]

其实分开写就是

\[ |\psi_2\rangle = \begin{cases}
(-1)^{f(0)}|+\rangle|-\rangle, \text{ if }f(0) \oplus f(1) = 0, \\
(-1)^{f(0)}|-\rangle|-\rangle, \text{ if }f(0) \oplus f(1) = 1. \\
\end{cases}\]

但是我们实在不喜欢\(|+\rangle\)和\(|-\rangle\)，还是更喜欢\(|0\rangle\)和\(|1\rangle\)。于是我们又在第一条输出线路上加了一个H门，把\(|+\rangle\)和\(|-\rangle\)转换回\(|0\rangle\)和\(|1\rangle\)。这样，\(|\psi_{3L}\rangle\)（就是\(|\psi_3\rangle\)中的第一个qubit，即右上角被测量的那个比特）就是：

\[ |\psi_{3L}\rangle = \begin{cases}
(-1)^{f(0)}|0\rangle, \text{ if }f(0) \oplus f(1) = 0, \\
(-1)^{f(0)}|1\rangle, \text{ if }f(0) \oplus f(1) = 1. \\
\end{cases}\]

这样我们只需要沿\(|0\rangle\)测量一下\(|\psi_{3L}\rangle\)，测出\(|0\rangle\)就说明\(f(0) \oplus f(1) = 0\)，反之就说明\(f(0) \oplus f(1) = 1\)，这样就可以100%确定\(f(0) \oplus f(1)\)的值了！至此就是Deutsch算法的内容。

神奇的地方在于：在量子版的算法中，我们只调用了一次\(U_f\)！而在传统计算机上，我们至少要调用两次\(f\)。你可能会说：差个常数2有啥大不了的嘛！确实，在Deutsch算法并没有在复杂度上体现出量子算法的优越性，但是接下来的Deutsch-Jozsa算法就能体现出本质上的差异了！

Deutsch-Jozsa算法

目标

有一个未知的黑盒\(f: \{0, 1\}^n \rightarrow \{0, 1\}\)，\(f\)可能有以下两种性质之一：

• f是常函数。
• f是均匀的（balanced）。这里均匀指的是：\(f(x)\)对于恰好一半的\(x\)得\(0\)，而对另恰好一半的\(x\)得\(1\)。

求\(f\)具有以上两种性质中的哪一种。

量子算法

Deutsch-Jozsa算法的电路图：

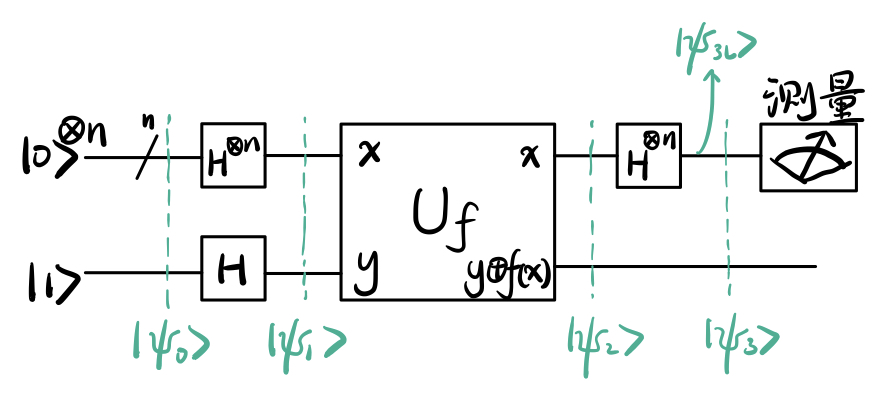
上面那“一条”线路实际上是\(n\)条，左上角的\(\not-^n\)符号表示这条线路代表\(n\)条线路。输入也随之变成了\(|\psi_0\rangle = |0\rangle^{\otimes n}|1\rangle\)。可以发现，Deutsch-Jozsa算法的电路图除了把第一条线路扩成了\(n\)条之外，和Deutsch算法的电路图并没有什么区别。（是不是突然有自信看懂了！）

让我们再用熟悉的方法，逐个计算\(|\psi_0\rangle, |\psi_1\rangle, |\psi_2\rangle, |\psi_3\rangle\)。

\[\begin{aligned}
|\psi_1\rangle &= (H|0\rangle^{\otimes n})(H|1\rangle) \\
&= \frac{1}{\sqrt2^n}(|0\rangle + |1\rangle)\otimes(|0\rangle + |1\rangle)\otimes\cdots\otimes(|0\rangle + |1\rangle)\otimes(|0\rangle - |1\rangle)/\sqrt2\\
&= \frac{1}{\sqrt2^n} \sum_{x\in \{0, 1\}^n} |x\rangle (|0\rangle - |1\rangle) / \sqrt2.\\
|\psi_2\rangle &= U_f |\psi_1\rangle = \frac{1}{\sqrt2^n} \sum_{x\in \{0, 1\}^n} (-1)^{f(x)} |x\rangle (|0\rangle - |1\rangle) / \sqrt2.
\end{aligned}\]

最后一步，我们要计算\(|\psi_{3L}\rangle = H|\psi_2\rangle\)。这一步稍微有点难算，再坚持一下！

考虑单个qubit\(x_1\)，有

\(H|x_1\rangle = \sum_{z_1 \in \{0, 1\}} (-1)^{x_1z_1} |z_1\rangle\)，

那么对\(n\)个qubit组成的\(|x\rangle\)，有

\[H|x\rangle = H|x_1 x_2 \cdots x_n\rangle = \sum_{z \in \{0, 1\}^n} (-1)^{\sum_i x_i z_i} |z\rangle / \sqrt2^n.
\]

所以

\[|\psi_{3L}\rangle = \frac{1}{\sqrt2^n} \sum_{x\in \{0, 1\}^n} (-1)^{f(x)} H|x\rangle = \frac1{2^n} \sum_{x \in \{0, 1\}^n} (-1)^{f(x)} \sum_{z \in \{0, 1\}^n} (-1)^{\sum_i x_i z_i} |z\rangle.
\]

接下来我们测量一下\(|\psi_{3L}\rangle\)，见证奇迹的时刻到了！

测得\(|0\rangle^{\otimes n}\)的概率是：

\[\langle \psi_{3L} | 0 \rangle \langle 0 | \psi_{3L} \rangle = \left(\frac1{2^n} \sum_{x\in \{0, 1\}^n} (-1)^{f(x)}\right)^2,
\]

因为除了\(| 0 \rangle\)以外的\(| z \rangle\)都和\(| 0 \rangle\)垂直，内积是0，所以其他项都没了，只剩下\(| z \rangle = | 0 \rangle\)的这一项。

当\(f\)是常函数时，所有\((-1)^{f(x)}\)都相等，\(\sum_{x\in \{0, 1\}^n} (-1)^{f(x)} = \pm 1\)，平方之后就等于\(1\)，所以测出\(|0\rangle^{\otimes n}\)的概率是1；

当\(f\)是均匀的函数时，一半\((-1)^{f(x)} = 1\)，另一半\((-1)^{f(x)} = -1\)，\(\sum_{x\in \{0, 1\}^n} (-1)^{f(x)} = 0\)，平方之后依然等于\(0\)，所以测出\(|0\rangle^{\otimes n}\)的概率是0。

这样，只需运行这个电路一次，就可以100%确定\(f\)的性质了！

一些常见的困惑

Q：啥是量子计算……啥是qubit……

A：反正大概是OI用不到的东西……Qiskit Textbook欢迎你！（再次免费打广告）

Q：不是啊，你连\(f\)是啥都不知道，你这个\(U_f\)咋从\(f\)构建出来的啊？

A：好问题！答案是，并不知道怎么构建……这个算法应用的场景其实是“给出一个量子黑盒\(U_f\)”，而不是给出\(f\)。（如果给出\(f\)，把\(f\)读进来、搞出一个真值表的复杂度就有\(2^n\)了……总之这个算法解决的问题不是这个。）

Q：只看上面那条线路，\(U_f\)对于\(|x\rangle\)不是相当于单位矩阵\(I_n\)一样，没有产生改变嘛？为啥第一条线路输出的不是\(H^{\otimes n}I_nH^{\otimes n}|0\rangle^{\otimes n} = |0\rangle^{\otimes n}\)呢？

A：好、好问题！问题出在“\(U_f\)对于\(|x\rangle\)相当于单位矩阵\(I_n\)”这句话上。事实上，\(U_f\)并不能写作\(I_n \otimes U_f'\)的形式，也就是说\(U_f\)并不能分成两个矩阵分别影响上下两条线路。

Q：我还是不明白。\(|x\rangle\)是\(|0\rangle^{\otimes n}\)经过H门后得到的，再经过一次H门为啥没变回去？？？

A：换种说法，经过\(U_f\)门之后，上下两条线路（\(|x\rangle\)和\(|y\rangle \oplus f(x)\)）发生了纠缠，所以\(U_f\)门输出的“两条线路”也无法分成“\(|x\rangle \otimes (|y\rangle \oplus f(x))\)”这样的“张量积”形式，因而不能分开单独考虑了。

Q：所以这个算法有啥用处吗？

A：它的用处大概是……帮你理解量子并行计算，证明量子并行计算与传统计算机相比有优越之处。现在看起来，Deutsch-Jozsa算法解决的问题或许没啥用处，但或许以后类似的方法能解决更重要的问题吧~（现学现卖，并未深入了解 =_=|||）

---

以上就是Deutsch-Jozsa算法的讲解啦，我也刚学，可能有很多错误，欢迎大佬指正！>v<