【BZOJ 1038】 1038: [ZJOI2008]瞭望塔

1038: [ZJOI2008]瞭望塔

Description

　　致力于建设全国示范和谐小村庄的H村村长dadzhi，决定在村中建立一个瞭望塔，以此加强村中的治安。我们
将H村抽象为一维的轮廓。如下图所示 我们可以用一条山的上方轮廓折线(x1, y1), (x2, y2), …. (xn, yn)来描
述H村的形状，这里x1 < x2 < …< xn。瞭望塔可以建造在[x1, xn]间的任意位置, 但必须满足从瞭望塔的顶端可
以看到H村的任意位置。可见在不同的位置建造瞭望塔，所需要建造的高度是不同的。为了节省开支，dadzhi村长
希望建造的塔高度尽可能小。请你写一个程序，帮助dadzhi村长计算塔的最小高度。

Input

　　第一行包含一个整数n，表示轮廓折线的节点数目。接下来第一行n个整数, 为x1 ~ xn. 第三行n个整数，为y1
 ~ yn。

Output

　　仅包含一个实数，为塔的最小高度，精确到小数点后三位。

Sample Input

【输入样例一】
6
1 2 4 5 6 7
1 2 2 4 2 1
【输入样例二】
4
10 20 49 59
0 10 10 0

Sample Output

【输出样例一】
1.000
【输出样例二】
14.500

HINT

N ≤ 300，输入坐标绝对值不超过106，注意考虑实数误差带来的问题。

【分析】

　　还没有AC就打题解真的好？【默默对拍中。。

　　题目里面没有图，奉献一幅可爱的图？（这是样例1）

　　

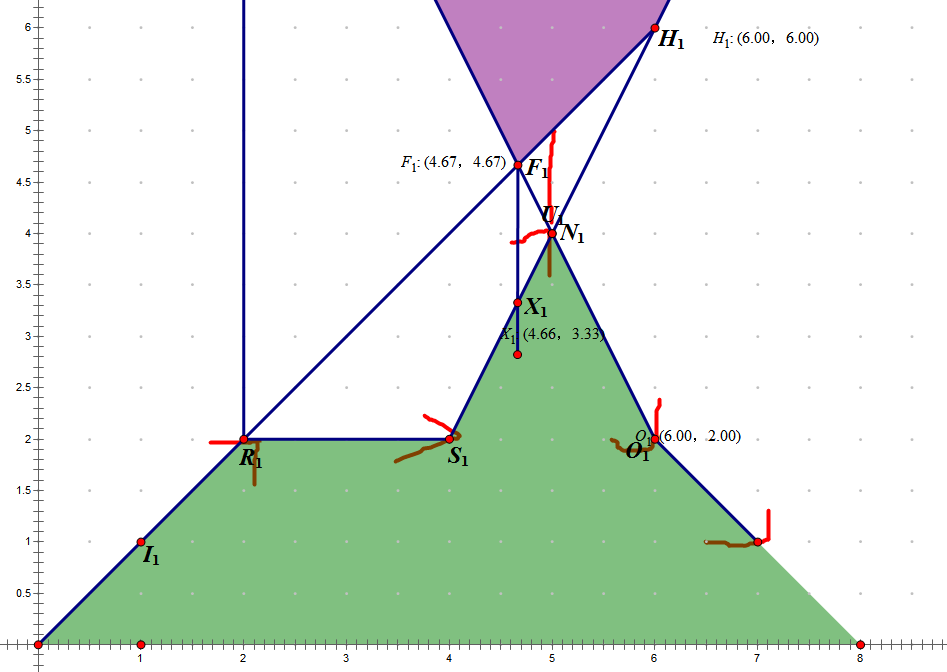
绿色是山，紫色是可行域，红色的是最小的塔高。

这题感觉吧跟多边形的核差不多，我们把轮廓线转换成半平面求角，然后考虑轮廓和半平面交的顶点（可以证明这里面一定存在最优塔高），

从这个顶点垂直于x轴延伸求出塔高，然后计算最小值就好了。

【1分钟后....

终于AC了，啊啊啊范围弄小了。。。。。10^6不是范围【没有听PO姐话就傻逼了一下

打半平面交的时候真是超级多错，最好弄eps搞精度。

然后注意轮廓和半平面交的边界（求塔高的时候不要越界，会有问题的）

就酱，真的是一周一题的缓慢速度。。。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 #define Maxn 310

 double INF=1e60;
 const double eps=0.000001;

 struct P {double x,y;};
 struct LN {P a,b;double slop;}l[Maxn],p[Maxn];

 double sx[Maxn],sy[Maxn];
 int n;

 P operator - (P x,P y)
 {
     P tt;
     tt.x=x.x-y.x;
     tt.y=x.y-y.y;
     return tt;
 }

 P operator + (P x,P y)
 {
     P tt;
     tt.x=x.x+y.x;
     tt.y=x.y+y.y;
     return tt;
 }

 P operator * (P x,double y)
 {
     P tt;
     tt.x=x.x*y;
     tt.y=x.y*y;
     return tt;
 }

 double Cross(P x,P y) {return x.x*y.y-x.y*y.x;}
 double Dot(P x,P y) {return x.x*y.x+x.y*y.y;}

 bool operator < (LN x,LN y) {return (x.slop==y.slop)?(Cross(x.b-x.a,y.b-x.a)<):(x.slop<y.slop);}

 P inter(LN x,LN y)
 {
     P nw=y.a-x.a;
     double tt;
     P X=x.b-x.a,Y=y.b-y.a;
     tt=Cross(nw,X)/Cross(X,Y);
     return y.a+Y*tt;
 }

 bool jud(LN x,LN y,LN z)
 {
     P nw=inter(x,y);
     if(Cross(z.b-z.a,nw-z.a)<eps&&Cross(z.b-z.a,nw-z.a)>-eps) return ;
     return Cross(z.b-z.a,nw-z.a)<;
 }

 int cnt;
 void op()
 {
     for(int i=;i<=cnt;i++)
     {
         printf("%.2lf %.2lf %.2lf %.2lf = %.2lf\n",l[i].a.x,l[i].a.y,l[i].b.x,l[i].b.y,l[i].slop);
     }printf("\n");
 }

 void opp(int L,int R)
 {
     for(int i=L;i<=R;i++)
     {
         printf("%.2lf %.2lf %.2lf %.2lf = %.2lf\n",p[i].a.x,p[i].a.y,p[i].b.x,p[i].b.y,p[i].slop);
     }printf("\n");
 }

 P as[Maxn];
 int L,R;

 bool ffind()
 {
     for(int i=;i<=n;i++) l[i].slop=atan2(l[i].b.y-l[i].a.y,l[i].b.x-l[i].a.x);
     sort(l+,l++n);

     cnt=;
     for(int i=;i<=n;i++)
     {
         if(l[i].slop!=l[cnt].slop) l[++cnt]=l[i];
     }
     // op();
     L=,R=;
     p[]=l[];p[]=l[];
         // opp(L,R);
     if(cnt<) return ;
     for(int i=;i<=cnt;i++)
     {
         while(R>L&&jud(p[R],p[R-],l[i])) R--;
         while(R>L&&jud(p[L],p[L+],l[i])) L++;
         p[++R]=l[i];
         // opp(L,R);
     }
     if(R>L&&jud(p[R],p[R-],p[L])) R--;
         // opp(L,R);
     if(R-L+<) return ;
     return ;
         // opp(L,R);
     /*double ans=INF;
     for(int i=L;i<R;i++)
     {
         P x=inter(p[i],p[i+1]);
         ans=ans<x.y?ans:x.y;
     }
     printf("%.3lf\n",ans);*/
 }

 void get_ans()
 {
     double ans=INF;
     int ft=L;
     P fx=inter(p[L],p[L+]);
     for(int i=;i<=n+;i++)
     {
         while(sx[i]>=fx.x&&ft<R)
         {
             ft++;
             fx=inter(p[ft],p[ft+]);
         }
         LN nw;
         nw.a.x=sx[i];nw.a.y=sy[i];
         nw.b.x=sx[i];nw.b.y=sy[i]+;
         P xx=inter(nw,p[ft]);
         ans=ans<xx.y-sy[i]?ans:xx.y-sy[i];
         // printf("==%.2lf\n",xx.y-sy[i]);
     }
         // printf("--%.2lf\n",ans);

     ft=;
     LN now;
     now.a.x=sx[];now.a.y=sy[];
     now.b.x=sx[];now.b.y=sy[];
     for(int i=L;i<R;i++)
     {
         P x=inter(p[i],p[i+]);
         if(x.x<sx[]) continue;
         while(x.x>=sx[ft+])
         {
             ft++;
             if(ft>n) break;
             // now.a.x=sx[ft];now.a.y=sy[ft];
             now.a=now.b;
             now.b.x=sx[ft+];now.b.y=sy[ft+];
         }
         if(ft>n) break;
         LN nw;
         nw.a=nw.b=x;nw.b.y=nw.b.y+;
         P xx=inter(nw,now);
         ans=ans<x.y-xx.y?ans:x.y-xx.y;
         // printf("==%.2lf\n",x.y-xx.y);
     }
     if(ans>=-eps&&ans<=eps) printf("0.000\n");
     else printf("%.3lf\n",ans);
 }

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%lf",&sx[i]);
     for(int i=;i<=n;i++) scanf("%lf",&sy[i]);
     n--;
     for(int i=;i<=n;i++)
     {
         l[i].a.x=sx[i];l[i].a.y=sy[i];
         l[i].b.x=sx[i+];l[i].b.y=sy[i+];
     }
     if(!ffind()) printf("0.000\n");
     else get_ans();
     return ;
 }

做几何题真的就不删调试了。

2016-12-29 17:09:28