UVA10054-The Necklace(无向图欧拉回路——套圈算法)
Time Limit: 3000 mSec
![]() Problem Description
Problem Description
Input
The input contains T test cases. The first line of the input contains the integer T. The first line of each test case contains an integer N (5 ≤ N ≤ 1000) giving the number of beads my sister was able to collect. Each of the next N lines contains two integers describing the colors of a bead. Colors are represented by integers ranging from 1 to 50.
![]() Output
Output
![]() Sample Input
Sample Input
![]() Sample Output
Sample Output
some beads may be lost
1 3
3 4
4 2
2 2
#include <bits/stdc++.h> using namespace std; #define REP(i, n) for (int i = 1; i <= (n); i++)
#define sqr(x) ((x) * (x)) const int maxn = + ;
const int maxm = + ;
const int maxs = + ; typedef long long LL;
typedef pair<int, int> pii;
typedef pair<double, double> pdd; const LL unit = 1LL;
const int INF = 0x3f3f3f3f;
const LL mod = ;
const double eps = 1e-;
const double inf = 1e15;
const double pi = acos(-1.0); int n, iCase;
int deg[maxn], gra[maxn][maxn]; void dfs(int u)
{
for (int i = ; i <= ; i++)
{
if (gra[u][i])
{
gra[u][i]--;
gra[i][u]--;
dfs(i);
cout << i << " " << u << endl;
}
}
} int main()
{
ios::sync_with_stdio(false);
cin.tie();
freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int T;
cin >> T;
while (T--)
{
cin >> n;
cout << "Case #" << ++iCase << endl;
memset(deg, , sizeof(deg));
memset(gra, , sizeof(gra));
int u, v;
for (int i = ; i < n; i++)
{
cin >> u >> v;
gra[u][v]++, gra[v][u]++;
deg[u]++, deg[v]++;
}
bool ok = true;
for (int i = ; i <= ; i++)
{
if (deg[i] % )
{
ok = false;
break;
}
}
if (!ok)
{
cout << "some beads may be lost" << endl;
}
else
{
dfs(v);
}
if (T)
cout << endl;
}
return ;
}
UVA10054-The Necklace(无向图欧拉回路——套圈算法)的更多相关文章
- UVa 10054 The Necklace(无向图欧拉回路)
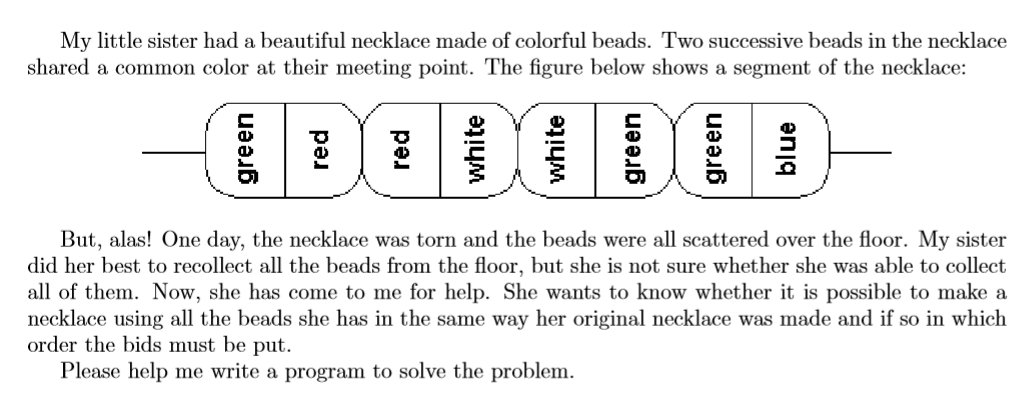
My little sister had a beautiful necklace made of colorful beads. Two successive beads in the neckla ...
- UVA-10054 The Necklace (欧拉回路)
题目大意:有n个珠子,珠子两边的颜色已知,问能否连成一条项链.(两个珠子可以项链当且仅当一个珠子的一边颜色与另一个珠子的另一边颜色相同). 题目分析:欧拉回路.将颜色视作节点,珠子当做边,问题变成了找 ...
- UOJ 117 欧拉回路(套圈法+欧拉回路路径输出+骚操作)
题目链接:http://uoj.ac/problem/117 题目大意: 解题思路:先判断度数: 若G为有向图,欧拉回路的点的出度等于入度. 若G为无向图,欧拉回路的点的度数位偶数. 然后判断连通性, ...
- UVA10054 The Necklace
UVA10054 The Necklace 链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=18806 [思路] 欧拉回路 ...
- SGU 455 Sequence analysis(Cycle detection,floyd判圈算法)
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=455 Due to the slow 'mod' and 'div' operati ...
- UVA 11549 CALCULATOR CONUNDRUM(Floyd判圈算法)
CALCULATOR CONUNDRUM Alice got a hold of an old calculator that can display n digits. She was bore ...
- UVA 11549 Calculator Conundrum (Floyd判圈算法)
题意:有个老式计算器,每次只能记住一个数字的前n位.现在输入一个整数k,然后反复平方,一直做下去,能得到的最大数是多少.例如,n=1,k=6,那么一次显示:6,3,9,1... 思路:这个题一定会出现 ...
- leetcode202(Floyd判圈算法(龟兔赛跑算法))
Write an algorithm to determine if a number is "happy". 写出一个算法确定一个数是不是快乐数. A happy number ...
- Floyd判圈算法
Floyd判圈算法 leetcode 上 编号为202 的happy number 问题,有点意思.happy number 的定义为: A happy number is a number defi ...
随机推荐
- Chapter 5 Blood Type——31
I stood carefully, and I was still fine. He held the door for me, his smile polite but his eyes mock ...
- Chapter 5 Blood Type——7
"You say that a lot," I noted, trying to ignore the sudden trembling in my stomach and kee ...
- JDBC 连接池的两种方式——dbcp & c3p0
申明:本文对于连接资源关闭采用自定义的 JDBCUtils 工具: package com.test.utils; import java.sql.Connection; import java.sq ...
- lua的String
基础字符串函数 字符串库中有一些函数非常简单,如: 1). string.len(s) 返回字符串s的长度: 2). string.rep(s,n) 返回字符串s重复n次的结果: 3 ...
- [转]BAT 批处理脚本 教程
第一章 批处理基础第一节 常用批处理内部命令简介 批处理定义:顾名思义,批处理文件是将一系列命令按一定的顺序集合为一个可执行的文本文件,其扩展名为BAT或者CMD.这些命令统称批处理命令.小知识:可以 ...
- Java 学习笔记 使用synchronized实现生产者消费者模式
说明 Object.wait()使当前的线程进入到等待状态(进入到等待队列) Object.notifyAll() 唤醒等待中的全部线程 Object.notify() 随机唤醒一个线程 代码 con ...
- Maven(十五)Maven 聚合
聚合解决的问题: 解决每个模块之间都要一个一个安装,一键安装各个模块工程 尤其时在配置继承后要先安装子模块在安装父,模块. 配置方式 自己找一个工程作为聚合工程,配置好后在聚合工程上运行Maven i ...
- JAVA-HashMap实现原理
一.HashMap实现原理 1. HashMap概述 HashMap是基于哈希表的Map接口的非同步实现.它允许存入null值和null键.它不保证存入元素的顺序与操作顺序一致,主要是不保证元素的顺序 ...
- 使用这些 HTTP 头保护 Web 应用
摘要: 安全是个大学问. 这是关于web安全性系列文章的第 三 篇,其它的可点击以下查看: Web 应用安全性: 浏览器是如何工作的 Web 应用安全性: HTTP简介 目前,浏览器已经实现了大量与安 ...
- 点击checkbox后,$(this).attr('checked')得到的值不会发生改变
这两天遇到一个问题,就是在点击checkbox后,$(this).attr('checked')得到的值要么是undefined,要么是checked,同一个表单一直点击却一点都不会发生改变,调试了一 ...
