James Munkres Topology: Sec 22 Exer 6

Exercise 22.6 Recall that \(\mathbb{R}_{K}\) denotes the real line in the \(K\)-topology. Let \(Y\) be the quotient space obtained from \(\mathbb{R}_K\) by collapsing the set \(K\) to a point; let \(p: \mathbb{R}_K \rightarrow Y\) be the quotient map.

(a) Show that \(Y\) satisfies the \(T_1\) axiom, but is not Hausdorff.

(b) Show that \(p \times p: \mathbb{R}_K \times \mathbb{R}_K \rightarrow Y \times Y\) is not a quotient map.

Comment This exercise shows that the product map of two quotient maps is not necessarily a quotient map.

Proof: (a) At first, we will clarify the forms of open sets in the quotient space \(Y\), which are defined as the images of saturated open sets in \(\mathbb{R}_K\) under the quotient map \(p\). Assume the set \(K\) coalesces to \(\alpha\), \(Y\) can be written as: \(Y = (\mathbb{R} - K) \cup \{\alpha\}\). For any \(x\) in \(\mathbb{R} - K\), \(p^{-1}(x) = x\) and \(p^{-1}(\alpha) = K\). Then the saturated open sets in \(\mathbb{R}_K\) have the following two forms:

1. open set \(U\) of \(\mathbb{R}_K\) which contains \(K\);
2. \(U - K\) with \(U\) being arbitrary open set in \(\mathbb{R}_K\).

Then their images under the quotient map \(p\) are

1. \((U - K) \cup \{\alpha\}\) with \(K \subsetneq U\)
2. \(U - K\)

which comprise the quotient topology on \(Y\). To prove \(Y\) satisfies the \(T_1\)-axiom, by referring to Theorem 17.8, we only need to show that one-point set \(\{x_0\}\) is closed. Then finite union of such closed singletons is also closed. To achieve this, there are two cases to be discussed.

1. If \(x_0 = \alpha\), for any point \(x \in Y\) and \(x \neq x_0\), i.e. \(x \in \mathbb{R} - K\), there exists an open set \(U - K\) in \(Y\) containing \(x\), which does not contain \(x_0\). Therefore, for all \(x \in \mathbb{R} - K\), it does not belong to the closure of \(\{\alpha\}\). Hence \(\{\alpha\}\) is closed.

2. If \(x_0 \in \mathbb{R} - K\), there are further two sub-cases:

   • For any \(x \in \mathbb{R} - K\) and \(x \neq x_0\), because \(\mathbb{R}_K\) is Hausdorff, there exists open sets \(U\) and \(V\) in \(\mathbb{R}_K\), such that \(x_0 \in U\), \(x \in V\) and \(U \cap V = \Phi\). Then \(x_0 \in (U - K)\), \(x \in (V - K)\) and \((U - K) \cap (V - K) = \Phi\), where both \(U - K\) and \(V - K\) are open in \(Y\). Hence \(\{x_0\} \cap (V - K) = \Phi\).

   • For \(x = \alpha\), the open set containing \(x\) has the form \((U - K) \cup \{\alpha\}\) where \(U\) is an open set in \(\mathbb{R}_K\) containing \(K\). Then,

     • when \(x_0 \in (-\infty, 0]\), let \(U = (0, 2)\);
     • when \(x_0 \in (0, 1]\), let \(U = (0,x_0) \cup (x_0, \frac{3}{2})\);
     • when \(x_0 \in (1, +\infty)\), let \(U = (0,x_0)\),

     such that \(K \subset U\) and \(\{x_0\} \cap ((U - K) \cup \{\alpha\}) = \Phi\).

   Combining the above two sub-cases, we have for any \(x \neq x_0\) in \(Y\), it does not belong to the closure of \(\{x_0\}\). Hence \(\{x_0\}\) is closed.

Summarize the above cases, one-point set in \(Y\) is closed. Hence \(Y\) satisfies the \(T_1\)-axiom.

Next, we will show \(Y​\) is not Hausdorff.

Let \(x_1, x_2 \in Y\), \(x_1 = \alpha\) and \(x_2 = 0\). For any open set in \(Y\) containing 0 but not \(\alpha\), it must have the form \(V - K\) with \(V\) being open in \(\mathbb{R}_K\). Then there exists an open interval \((a_2, b_2)\) with \(a_2 < 0\) and \(b_2 > 0\) such that \(0 \in (a_2, b_2)\) and \((a_2, b_2) \subset V\). We can find an \(n_0 \in \mathbb{Z}_+\) such that \(\frac{1}{n_0} < b_2\) and hence \(\frac{1}{n_0} \in (a_2, b_2)\). Meanwhile, any open set containing \(\alpha\) has the form \((U - K ) \cup \{\alpha\}\) with \(U\) being open in \(\mathbb{R}_K\) and \(K \subsetneq U\). Then there exists an open interval \((a_1,b_1)\) such that \(\frac{1}{n_0} \in (a_1, b_1)\) and \((a_1, b_1) \subset U\). Therefore, \((a_1,b_1) \cap (a_2,b_2) \neq \Phi\) and \(U \cap V \neq \Phi\), especially, \((U-K)\cap(V-K)\neq\Phi\). Hence, \(((U-K)\cup\{\alpha\}) \cap (V-K) \neq \Phi\). Therefore, for any open set containing 0, there is no open set containing \(\alpha\) which has no intersection with it. So \(Y\) is not Hausdorff.

(b) To prove this part, Exercise 13 in Section 17 should be adopted, which is presented below:

\(X\) is Hausdorff if and only if the diagonal \(\Delta = \{x \times x \vert x \in X \}\) is closed in \(X \times X\).

1. If \(X\) is Hausdorff, for any \(x_1, x_2 \in X\) and \(x_1 \neq x_2\), there exist \(U\) and \(V\) open in \(X\) such that \(x_1 \in U\), \(x_2 \in V\) and \(U \cap V = \Phi\). Because \(U\) and \(V\) have no common points, \((U \times V) \cap \Delta = \Phi\). Then according to Theorem 17.5, \((x_1, x_2)\) does not belong to the closure of \(\Delta\). Because \(x_1\) and \(x_2\) are arbitrary two different points in \(X\), \(\Delta\) is closed.
2. On the contrary, if \(\Delta\) is closed, for all \(x_1, x_2 \in X\) and \(x_1 \neq x_2\), there exists an open set \(W\) in \(X \times X\) containing \((x_1,x_2)\) such that \(W \cap \Delta = \Phi\). Then there exists a basis element \(U \times V\) in \(X \times X\) such that \((x_1, x_2) \subset U \times V \subset W\). Hence \(x_1 \in U\) and \(x_2 \in V\). Because \((U \times V) \cap \Delta = \Phi\), \(U \cap V = \Phi\). Because \(x_1\) and \(x_2\) are arbitrary two different points in \(X\), \(X\) is Hausdorff.

With the proved S17E13 and the obtained conclusion in part (a) that \(Y\) is no Hausdorff, we know that the diagonal set \(\Delta\) is not closed in \(Y \times Y\). Meanwhile, because its preimage \((p \times p)^{-1}(\Delta) = \{x \times x \vert x \in \mathbb{R}\}\) is closed in \(\mathbb{R}_K \times \mathbb{R}_K\), the product map \(p \times p\) is not a quotient map.

Finally, the following figure illustrates the original space \(\mathbb{R}_K\) and the quotient space \(Y\). The transformation from \(\mathbb{R}_K\) to \(Y\) can be considered as merging a countable number of knots on a rope.

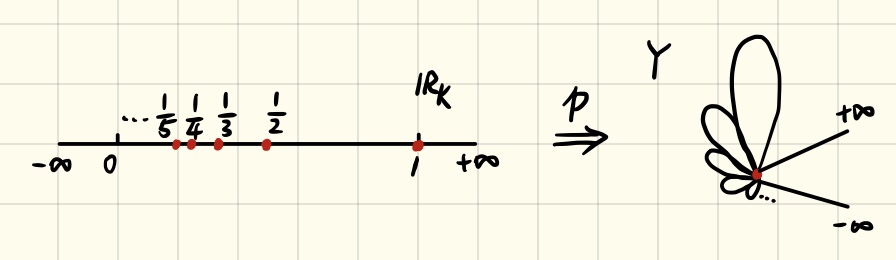
PS: Because the world we are living in is Hausdorff, Diagon Alley is always closed.