bzoj1997 [HNOI2010]平面图判定Plana

bzoj1997 [HNOI2010]平面图判定Planar

链接

bzoj

luogu

思路

好像有很多种方法过去。我只说2-sat

环上的边，要不在里面，要不在外边。

有的边是不能同时在里面的,可以O(m^2)的连边

但是m是10000，不过平面图内边数不得超过3*n-6,

m太大的直接NO就好了，其他的n,m是一个数量级的，直接2-sat暴力连边做就好了。

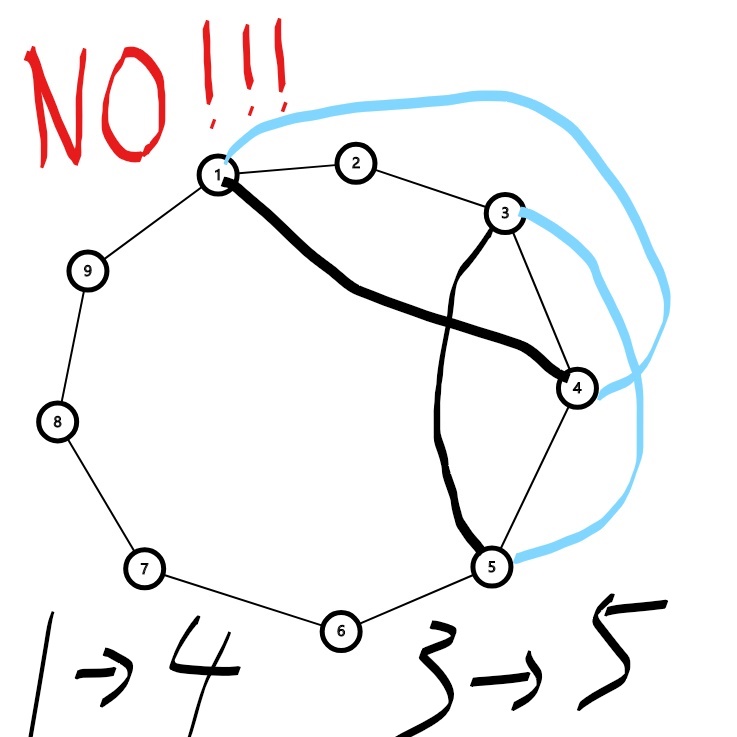
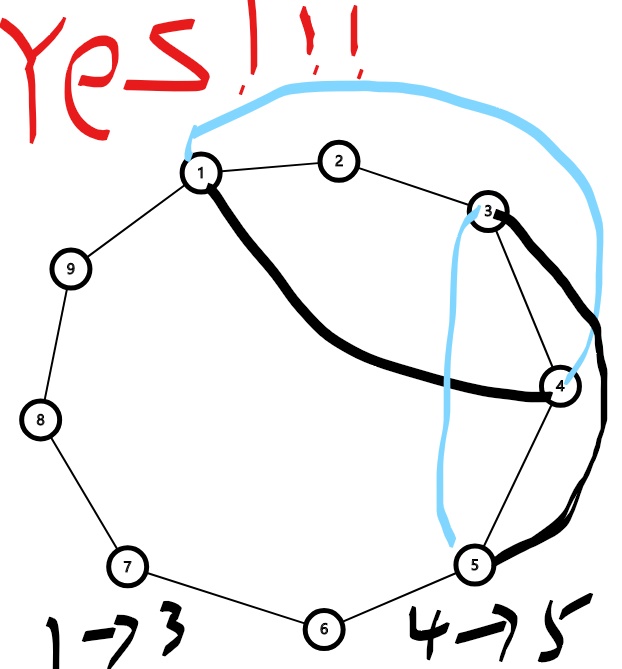
细节

双向边

是边m进行2-sat，不是点n

代码

#include <bits/stdc++.h>
using namespace std;
const int N=1207;
int read() {
    int x=0,f=1;char s=getchar();
    for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
    for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
    return x*f;
}
int n,m,a[N],u[10005],v[10005],tong[N],rk[10005];
struct node {int v,nxt;}e[N*N*2];
int head[N],tot;
map<pair<int,int >,int > Hash;
void add(int u,int v) {
    e[++tot].v=v;
    e[tot].nxt=head[u];
    head[u]=tot;
}
int low[N],dfn[N],cnt,stak[N],top,vis[N],col,belong[N];
void tarjan(int u) {
    dfn[u]=low[u]=++cnt;
    vis[u]=1;
    stak[++top]=u;
    for(int i=head[u];i;i=e[i].nxt) {
        int v=e[i].v;
        if(!dfn[v]) {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        } else if(vis[v]) {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u]) {
        ++col;
        while(stak[top]!=u) {
            vis[stak[top]]=0;
            belong[stak[top]]=col;
            top--;
        }
        vis[u]=0;
        belong[u]=col;
        top--;
    }
}
void clear() {
    tot=cnt=col=0;
    Hash.clear();
    memset(head,0,sizeof(head));
    memset(low,0,sizeof(low));
    memset(dfn,0,sizeof(dfn));
    memset(rk,0,sizeof(rk));
}
void solve() {
    clear();
    n=read(),m=read();
    for(int i=1;i<=m;++i) u[i]=read(),v[i]=read();
    for(int i=1;i<=n;++i) a[i]=read();
    for(int i=2;i<=n;++i) {
        rk[a[i]]=i;
        Hash[make_pair(a[i],a[i-1])]=1;
        Hash[make_pair(a[i-1],a[i])]=1;
    }
    Hash[make_pair(a[1],a[n])]=1;
    Hash[make_pair(a[n],a[1])]=1;
    if(m>3*n-6) return puts("NO"),void();
    for(int i=1;i<=m;++i) {
        if(!Hash[make_pair(u[i],v[i])]) {
            memset(tong,0,sizeof(tong));
            for(int j=1,flag=0;j<=n;++j) {
                if(u[i]==a[j]||v[i]==a[j]) flag=flag^1;
                tong[j]=flag;
            }
            for(int j=i+1;j<=m;++j) {
                if(Hash[make_pair(u[j],v[j])]) continue;
                if(u[i]==v[j]||u[i]==u[j]||v[i]==v[j]||v[i]==u[j]) continue;
                if(tong[rk[u[j]]]^tong[rk[v[j]]]) {
                    add(i,j+m);
                    add(j+m,i);
                    add(i+m,j);
                    add(j,i+m);
                }
            }
        }
    }
    for(int i=1;i<=2*m;++i)
        if(!dfn[i])
            tarjan(i);
    for(int i=1;i<=m;++i)
        if(belong[i]==belong[i+m])
            return puts("NO"),void();
    return puts("YES"),void();
}
int main() {
    for(int T=read();T;T--) solve();
    return 0;
}