Rabin算法

中国剩余定理

如果已知n的素因子，那么就能够利用中国剩余定理求解方程组。用现代数学的语言来说明就是，中国剩余定理给出了以下的一元线性同余方程组有解的判定条件：

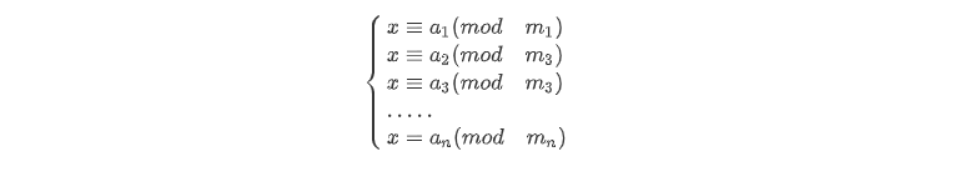
一般而言，如果n的素因子可以分解为:
\[
n=p_1 * p_2 * ... * p_t
\]

那么方程组：
\[
(x \quad mod \quad p_i)=a_i \quad (i=1,2,...t)
\]
有唯一解，这里x<n，就是说一个数被他的余数模这些素数唯一确定

例如，去两个素数2和5，与一个数字9，那么9 mod 2=1，9 mod 5=4，则小于2*5=10且满足上式的只有9

所以能够得到如果对已任意的a<p，b<q（p,q都是素数），那么，当x<p*q的时候，存在一个唯一的x使得：
\[
x \equiv a(mod \quad p)\quad 且\quad x\equiv b(mod \quad q)
\]
如何计算x？

首先通过欧几里得算法找到u，使得：
\[
u * q \equiv 1(mod \quad p)
\]
然后计算：
\[
x=(((a-b) * u) mod \quad p)*q+b
\]
推论：

如果p和q都是素数，且 p<q，那么存在一个唯一的x<p*q，使得
\[
a \equiv x(mod \quad p)且b \equiv x(mod \quad q)
\]
如果\(a \ge b\quad mod \quad p\)，那么：
\[
x = (((a-(b \quad mod \quad p)) * u)mod \quad p) * q + b
\]
如果\(a < b\quad mod \quad p\)，那么：
\[
x = (((a+p-(b \quad mod \quad p)) * u)mod \quad p) * q + b
\]

二次剩余

如果p是素数，且a<p，如果
\[
x^2 \equiv a(mod \quad p) \quad 对某些x成立
\]
那么称a是对模p的二次剩余

而如果a是对模n的一个二次剩余，那么它必定是对模n的所有因子的二次剩余，例如

如果p=7，那么二次剩余是1、2、4

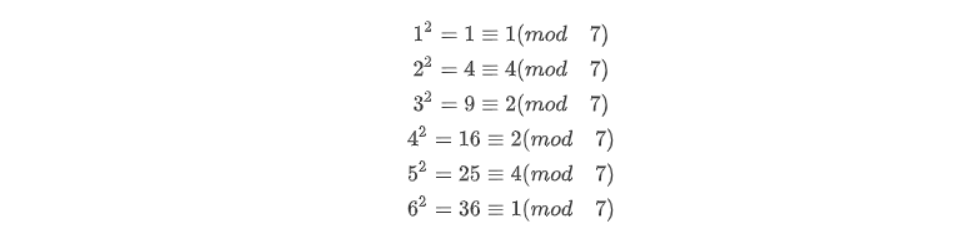
每一个二次剩余都在上面出现了两次

而对于下面的的方程：

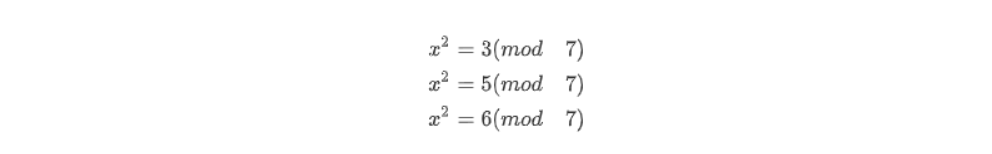
不存在一个x的值能够满足任意一个，所以对模7的非二次剩余就是3、5、6

费马小定理

如果m是一个素数，且a不是m的倍数，那么根据费马小定理，有：
\[
a^{m-1} \equiv 1(mod \quad m)
\]

欧拉函数

也称之为\(\varphi\)函数，写作\(\varphi(n)\)，\(\varphi(n)\)表示与n互素的小于n的正整数的数目

如果n是素数，那么\(\varphi(n)=n-1\)，如果\(n=pq\)，（p、q为素数）那么\(\varphi(n)=(p-1)(q-1)\)

根据费马小定理的欧拉推广，如果`gcd(a，n)=1，那么：
\[
a^{\varphi(n)}\quad mod\quad n=1
\]

Rabin算法

破解RSA的关键即在于大整数的分解，只要n被成功分解，就能够破译。而Rabin密码体制是对RSA的一种修正。

1. Rabin密码体制对于同一密文，可能有两个以上对应的明文
2. 破译该密码体制同样等价于对大整数的分解，RSA中选取的公钥e满足\(1<e<\varphi(n)\)，而Rabin中则选取e=2

密钥的产生

1. 随机选择两个大素数 p，q，通常选取p，q\(\equiv 3(mod \quad4)\)

2. 密钥为p，q

3. 公钥n=p*q

4. 明文：m，密文：c

5. 加密：\(c \equiv m^2 \quad mod \quad n\)

6. 解密过程如下：

   1. \(m_p=c^{\frac{p+1}{4}}mod \quad p\)

      \(m_q=c^{\frac{q+1}{4}}mod \quad q\)

   2. 使用扩展欧几里得算法得到\(y_p和y_q\)，使得\(y_p·p+y_q·q=1\)

   3. 利用中国剩余定理得到

      \(x_1=(y_p·p·m_q+y_q·q·m_p) mod \quad n\)

      \(x_2=n-x_1\)

      \(x_3=(y_p·p·m_q-y_q·q·m_p) mod \quad n\)

      \(x_4=n-x_3\)

   4. 举例

      a. 假定计算：\(p=7，q=11，n=77，m=20\)

      b. 那么：\(c=m^2 \quad mod \quad n=400 \quad mod \quad 77=15\)

      c. 所以：

      ​ \(m_p=c^{\frac{p+1}{4}}mod \quad p=15^2 \quad mod \quad 7=1\)

      ​ \(m_q=c^{\frac{q+1}{4}}mod \quad q=15^2 \quad mod \quad 11=9\)

      d. 利用扩展欧几里得算法计算\(y_p·p+y_q·q=1；y_p=-3，y_q=2\)

      e. 最终得到：

   ​ \(x_1=(y_p·p·m_q+y_q·q·m_p) mod \quad n=(-3·7·9+2·11·1)mod 77=64\)

   ​ \(x_2=n-x_1=77-64=13\)

   ​ \(x_3=(y_p·p·m_q-y_q·q·m_p) mod \quad n=(-3·7·9-2·11·1)mod 77=20\)

   ​ \(x_4=n-x_3=77-20=57\)

参考

《应用密码学》(协议、算法与C源程序)：https://item.jd.com/11362600.html

维基百科：https://en.wikipedia.org/wiki/Rabin_cryptosystem