P1070道路游戏题解

日常吐槽

作为hin久hin久以前考试考到过的一道题窝一直咕咕咕到现在才想起来去做因为讲解都忘干净了然后自己重新考虑发现被卡了3天

题面

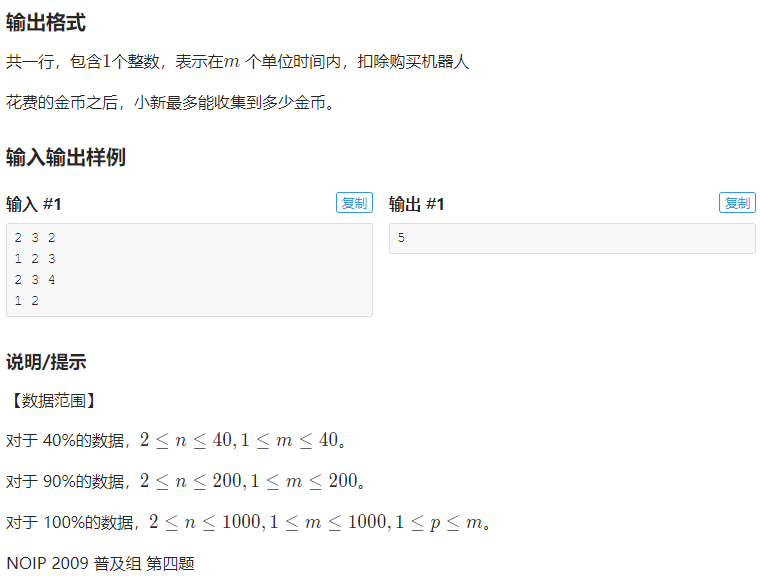
看到题目发现这题的dp状态似乎有点不是很明确？

我们来理一理题目的限制以及我们要干什么。

每条路上出现的金币数量受时间和地点的限制。所以我们至少要用到一个二维的东西。

题目中说当机器人消失的时候需要在任意一个工厂购买机器人。我们先以可能TLE的思路进行dp。设\(dp[i][j]\)表示在\(i\)时刻到达工厂\(j\)的最大值。我们要枚举从哪个点走到了\(j\)点，同时因为购买地点的选取是任意的，所以要加上\(max\{ f[i-k][j]\),那么\(dp[i][j]=max\{max\{ f[i-k][j] \},gold(d,j,i-k,i)-cst[d]\}\),其中\(gold(d,j,i-k,i)\)表示在\(i-k\)时刻一直到\(i\)时刻，从\(d\)点走到\(j\)点路上的所有金币。但这个肯定是会\(T\)的，我们发现地点这一维是最耗复杂度的（它整整占用了两层\(for\)），于是果断删掉。

于是我们设\(dp[i]\)表示\(i\)时刻的最大收益，但是去掉地点这一维了，上面的\(gold\)就必须预处理。

设\(sum[i][j]\)表示在时刻\(i\),从0时刻的第1个工厂走到了第\(j\)个工厂的能捡到的金币，即不扣除买机器人的钱（在哪里买机器人是\(dp\)中要干的事，这里只是预处理）。在这里设\(money[i][j]\)表示时刻\(j\)，第\(i\)条路上出现的金币数量。那么\(sum[i][j]=sum[i-1][jian(j,1)]+money[jian(j,1)][i]\)。其中\(jian(i,j)\)表示\(j\)工厂往前走\(i\)步到达的工厂。

辣么转移方程也就呼之欲出了。\(dp[i]=max\{ dp[i-j]+sum[i][k]-sum[i-j][jian(k,j)]-cst[jian(k,j)]\}\),\(cst[i]\)表示在第\(i\)个工厂购买机器人花的钱。

代码:

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<map>
#include<ctime>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i128;
const int inf=2147483647;
inline int read()
{
	char ch=getchar();
	int x=0;
	bool f=0;
	while(ch<'0'||ch>'9')
	{
		if(ch=='-') f=1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9')
	{
		x=(x<<3)+(x<<1)+(ch^48);
		ch=getchar();
	}
	return f?-x:x;
}
int n,m,p,mon[1009][1009],cst[1009];
int dp[1009],sum[1009][1009];
inline int jian(int i,int k)
{
	int qwq=(i-k+n)%n;
	return qwq?qwq:n;
}
int main()
{
   freopen("1.in","r",stdin);
	n=read();m=read();p=read();
	for(int i=1;i<=n;i++)
	 for(int j=1;j<=m;j++)
	  mon[i][j]=read();//money在这里简写为mon
	for(int i=1;i<=n;i++)
	 cst[i]=read();
	for(int i=1;i<=m;i++)
	 for(int j=1;j<=n;j++)
	  sum[i][j]=sum[i-1][jian(j,1)]+mon[jian(j,1)][i];//,printf("sum[%d][%d]=%d\n",i,j,sum[i][j]);
    memset(dp,-0x3f,sizeof(dp));
    dp[0]=0;
	for(int i=1;i<=m;i++)
    {
    	for(int j=1;j<=p;j++)//枚举步数
		{
			for(int k=1;k<=n;k++)//枚举地点
	         if(i-j>=0)
			  dp[i]=max(dp[i],dp[i-j]+sum[i][k]-sum[i-j][jian(k,j)]-cst[jian(k,j)]);
		}
	}
	printf("%d",dp[m]);
}

我们发现上面的方程需要枚举地点，它是个三维的，会\(TLE\)(当然因为现在机子跑的快是可以卡过的),我们要想办法优化。

时间肯定是不能省略的，那剩下的就是步数和地点。我们肯定要把一维优化掉。思考哪个看起来更好搞一些。地图是个环，看起来很麻烦的亚子，所以我们把步数优化掉。

把方程中不需要枚举步数的项提出来：

\(dp[i]=max\{dp[i-j]-sum[i-j][jian(k,j)]-cst[jian(k,j)]\}+sum[i][k]\)

由于步数是要被优化掉的，所以我们保留时间和地点两个状态，设置辅助变量\(qwq[i][j]=dp[i]-sum[i][j]-cst[j]\)

新的方程：\(dp[i]=max\{qwq[i-k][j-k]\}+sum[i][j]\)，其中k枚举步数,我们要优化掉这一维，发现第二维每次枚举的时候会+1,于是可以各种乱搞

由于博主用不优化的代码卡过了所以优化代码先咕咕咕叭

(逃）(害怕被打.jpg) 跟我读：可持久化咕咕咕