[2019杭电多校第二场][hdu6598]Harmonious Army(最小割)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6598

题意是说一个军队有n人，你可以给他们每个人安排战士或者法师的职业，有m对人有组合技，组合技的信息是A,B,C，代表如果这两个人是两个战士，则组合技威力为A，一个战士一个法师，威力为B，其中B=A/4+C/3，两个法师，威力为C，求最大的威力。

很网络流的题目，那就流呗XD

先考虑如果每个人可以选择两个职业，则威力为$sum=\sum_{i=1}^{n}(a[i]+b[i]+c[i])$

如果不能选择两个职业,则可以看成选择两个职业的答案减去网络中的最小割。

则我们向着最小割的方向思考。

然后我们先考虑连通性，即所有点连战士(看成源点)和法师(看成汇点)，并且有关系的点相互连接。

然后看下面的图(s为源点，t为汇点，x,y为一对关系)

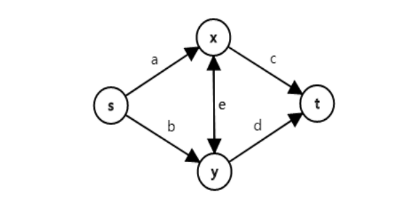
然后考虑权值：

如果x选择战士,y选择战士，则a+b=B+C(割掉B,C的威力)

如果x选择法师,y法师战士，则c+d=B+A(割掉A,B的威力)

如果x选择战士,y选择法师，则a+e+d=A+C(割掉A,C的威力)

如果x选择法师,y选择战士，则b+e+c=A+C(割掉A,C的威力)

然后可以得到一组解a=b=(A+B)/2，c=d=(C+B)/2,e=(A+C)/2-B。

然后就可以愉快的建图。

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<string>
 #include<queue>
 using namespace std;
 typedef long long ll;
 const int maxn = 2e5 + ;
 const ll inf = 1e18;
 struct node {
     int e, next;
     double w;
 }edge[maxn];
 int head[maxn], len;
 int d[maxn];
 void init() {
     memset(head, -, sizeof(head));
     len = ;
 }
 void add(int s, int e, double  w) {
     edge[len].e = e;
     edge[len].w = w;
     edge[len].next = head[s];
     head[s] = len++;
 }
 bool bfs(int s, int e) {
     queue<int>q;
     memset(d, , sizeof(d));
     d[s] = ;
     q.push(s);
     while (!q.empty()) {
         int x = q.front(); q.pop();
         for (int i = head[x]; i != -; i = edge[i].next) {
             int y = edge[i].e;
             if (edge[i].w && !d[y]) {
                 d[y] = d[x] + ;
                 q.push(y);
             }
         }
     }
     return d[e];
 }
 double dfs(int x, int e, double limit) {
     if (x == e)
         return limit;
     double add, ans = ;
     for (int i = head[x]; i != -; i = edge[i].next) {
         int y = edge[i].e;
         if (d[y] == d[x] +  && edge[i].w) {
             add = dfs(y, e, min(edge[i].w, limit));
             edge[i].w -= add;
             edge[i ^ ].w += add;
             ans += add;
             limit -= add;
             if (!limit)
                 break;
         }
     }
     if (!ans)
         d[x] = -;
     return ans;
 }
 double dinic(int s, int e) {
     double ans = ;
     while (bfs(s, e))
         ans += dfs(s, e, inf);
     return ans;
 }
 int main() {
     int n, m;
     while (scanf("%d%d", &n, &m) != EOF) {
         init();
         int s = n + , t = n + ;
         ll sum = ;
         for (int i = ; i <= m; i++) {
             ll x, y;
             double a, b, c;
             scanf("%lld%lld%lf%lf%lf", &x, &y, &a, &b, &c);
             add(s, x, (a + b) / );
             add(x, s, );
             add(s, y, (a + b) / );
             add(y, s, );
             add(x, t, (b + c) / );
             add(t, x, );
             add(y, t, (b + c) / );
             add(t, y, );
             add(x, y, -b + (a + c) / );
             add(y, x, );
             add(y, x, -b + (a + c) / );
             add(x, y, );
             sum += a + b + c;
         }
         ll ans = round(sum - dinic(s, t));
         printf("%lld\n", ans);
     }
 }