shell练习--PAT题目1007：关于素数对（失败案例）

让我们定义d​n​​为：d​n​​=p​n+1​​−p​n​​，其中p​i​​是第i个素数。显然有d​1​​=1，且对于n>1有d​n​​是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。

现给定任意正整数N(<)，请计算不超过N的满足猜想的素数对的个数。

输入格式:

输入在一行给出正整数N。

输出格式:

在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:

20

输出样例:

4

这个题目，我一直没弄明白，然后走了很多逻辑误区，然后用了很多for的循环来判断。
基本思路：
　　1.定义函数，用来判断数字x是不是素数；
　　2.循环判断 输入的数字 n 的范围数字 2<=x<=n 是不是素数，然后放入一个数组中；
　　3.判断ss[i+1]-ss[i]是否=2 等于则+1；

#!/bin/bash

func_sushu(){
for (( i=2 ;i < $x; i++ ))   #最小的素数为2，所以以2作为起点
do
        cond=true
        if [[ $(expr $x % $i) -eq 0 ]]
        then
                cond=false
                break
        fi
done

if $cond  #判断状态变量，如果存在false，则为非素数
then
        return 0
else
        return 1
fi
}

read  -p " input number:" n

(( $n - 0)) && if [ $? -ne 0 ] || [ $n -lt 2 -o $n -gt 1000000 ];then echo "$n is not need!" ;exit 1 ;fi

count=1
ss[0]=2 #2是最小的素数
for ((j = 3 ; j <= $n ; j++))
do
        x=$j
        func_sushu
        if [ $? -eq 0 ]
        then
                ss[$count]=$j
                let count++
        else
                continue
        fi
done

echo ${ss[@]}

i=0
sum=0
for ((i>=0;i<$n;i++ ))
do
        num1=`echo ${ss[$(expr $i + 1)]}`
        num2=`echo ${ss[$i]}`
        if [ -n "$num1" ]  #这里对于非空的判断需要加双引号，不然会出现判断 ] 的逻辑错误
        then
                if [ $(expr $num1 - $num2) -eq 2 ]
                then
                        let sum++
                fi
        else
                break
        fi
done
echo $sum

太感动了，居然只有一个绿

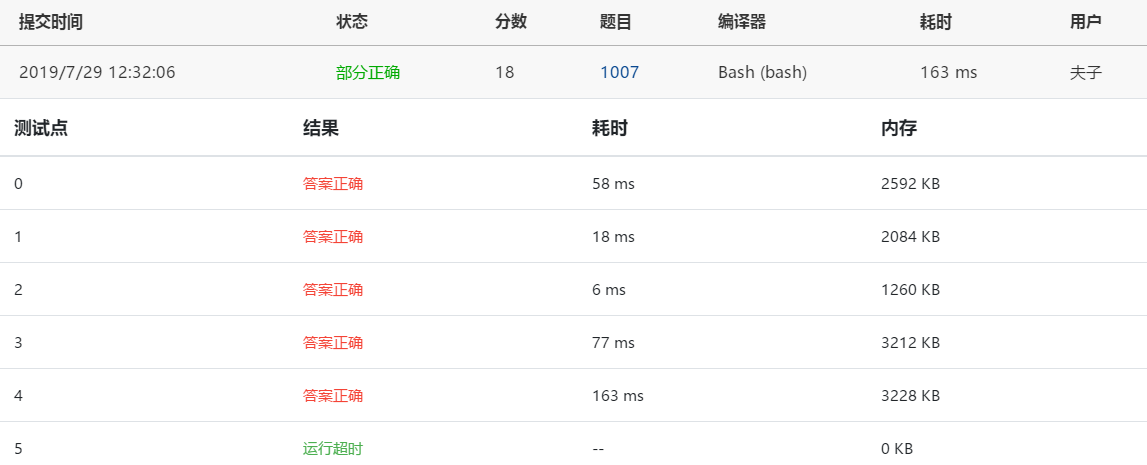
现在基本获取了想要的结果了，但是需要优化

　　1.去掉多余的代码；

　　2.用 j <= $n的平方根的逻辑判断是否为素数（参照其他代码）；--运行超时的问题

#!/bin/bash

func_sushu(){
local count=1
ss[0]=2
for ((j = 3 ; j <= $n ; j++))
do
        for (( i=2 ;i <= $(echo "scale=0 ;sqrt($j)" |bc ); i++ ))
        do
                cond=true
                if [[ $(expr $j % $i) -eq 0 ]]
                then
                        cond=false
                        break
                fi
        done
        if $cond
        then
                ss[$count]=$j
                let count++
        else
                continue
        fi
done
}

read  -p "input number:" n
(( $n - 0)) && if [ $? -ne 0 ] || [ $n -lt 2 -o $n -gt 1000000 ];then echo "$n is not need!" ;exit 1 ;fi
func_sushu
i=0
sum=0
for ((i>=0;i<$n;i++ ))
do
        if [ -n "`echo ${ss[$(expr $i + 1)]}`" ] && [ $(expr $(echo ${ss[$(expr $i + 1)]}) - $(echo ${ss[$i]})) -eq 2 ]
        then
                let sum++
        else
                continue
        fi
done
echo $sum

　　阿希吧，五红变1红