一本通【例题4】Addition Chains——题解

又是一道剪枝剪了半天的搜索题。。。题目传送

要充分利用题目中的约束条件：1、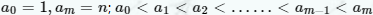；2、对于每个k(1≤k≤m)k(1≤k≤m)满足ak=ai+aj(0≤i,j≤k−1)ak=ai+aj(0≤i,j≤k−1),这里i与j可以相等。由此可以推出a1一定=2(也能减少很多操作次数了吧)

还是先找找搜索过程要面临的状态和有关维度：目标数n,答案序列的长度limit，序列中的每个数ai，当前序列中的最后一个数last。

由于如果不对序列长度加以限制，普通的深搜便会“一发不可收拾”，所以这里用迭代加深搜索。

可行性剪枝考虑：

　　　1、由于迭代加深搜索会把之前的状态全搜索一遍，所以应当限制一下limit的下界。注意到长度为k的序列能最大造出来的数为2^k-1，所以序列最短应保证那个最大造出来的数>=n，预处理就行。

考虑一下搜索顺序：因为n是由小数加小数构造出来的，求最小的构造次数。因此应从大到小搜索。

考虑防等效冗杂：让从大到小枚举的两个数中的第1个正常枚举、第2个从第1个开始枚举。

继续考虑可行性剪枝：

　　　2、当前枚举的序列里的两个数相加应大于last，只有这样才能继续搜索。

　　　3（效率还不够，更近一步考虑一下未来）：发现一个序列最大的增长方式即为让序列中最后一个数自己加自己，设这个数为a，进行k次这样的增长后序列中最后的一个数则为a*2^k，每次增长操作都会增加一个数。对于当前长度为l的序列，如果last*2^limit-l仍小于n，就回溯；等于n，那limit一定是答案；大于n时才继续搜索。2的幂次方可打表或预处理出。

最优性剪枝：找到答案就停止就行。

AC代码：

 #include<iostream>
 #include<cstdio>

 using namespace std;

 int n,a[],bj,cankao[],mi[];

 void dfs(const int &limit,int k)//要填第k个(k从1开始）
 {
     if(bj) return;
     if(k==limit)
     {
         for(int i=k-;i>=;i--)
             for(int j=i;j>=;j--)
             {
                 if(a[i]+a[j]==n)
                 {
                     a[k-]=n;
                     bj=;
                     return;
                 }
             }
     }
     if(a[k-]*mi[limit-k+]<=n)//可行性剪枝3
     {
         if(a[k-]*mi[limit-k+]==n)
         {
             bj=;
             for(int j=k-;j<limit;j++)
             a[j]=a[j-]*;
         }
         return;
     }
     for(int i=k-;i>=;i--)
     {
       for(int j=i;j>=;j--)//防等效冗杂
         if(a[i]+a[j]>a[k-])
         {
             if(a[i]+a[j]>=n) continue;//可行性剪枝2
             a[k-]=a[i]+a[j];
             dfs(limit,k+);
             if(bj) return;
         }
         else
         {
             if(j==i) return;
             break;
         }
     }
 } 

 void work()
 {
     bj=;
     for(int len=cankao[n];len<=n;len++)
     {
         dfs(len,);
         if(bj)
         {
             for(int i=;i<len;i++)
                 printf("%d ",a[i]);
             putchar('\n');
             return;
         }
     }
 }

 void init()
 {
     int i=,step=;
     while(i<=)
     {
         cankao[i]=step;
         i*=;
         step++;
     }
     for(i=;i<=;i++)
         if(!cankao[i])
             cankao[i]=cankao[i-];//以上为可行性剪枝1
     i=,step=;
     mi[]=;
     for(int j=;j<=;j++)//2的幂次方的预处理
     {
         i*=;
         mi[j]=i;
     }
 }

 int main()//预处理
 {
     init();
     a[]=;a[]=;//注意序列下标0开始
     scanf("%d",&n);
     while(n)
     {
         if(n==)//处理特殊情况
         {
             putchar('');
             putchar('\n');
         }
         if(n==)
             cout<<"1 2\n";
         if(n>=)
         work();
         scanf("%d",&n);
     }
     return ;
 }