【BZOJ2070】列队春游———[组合数学+概率DP]

数学渣滓不可做の题OTZ

Description

---

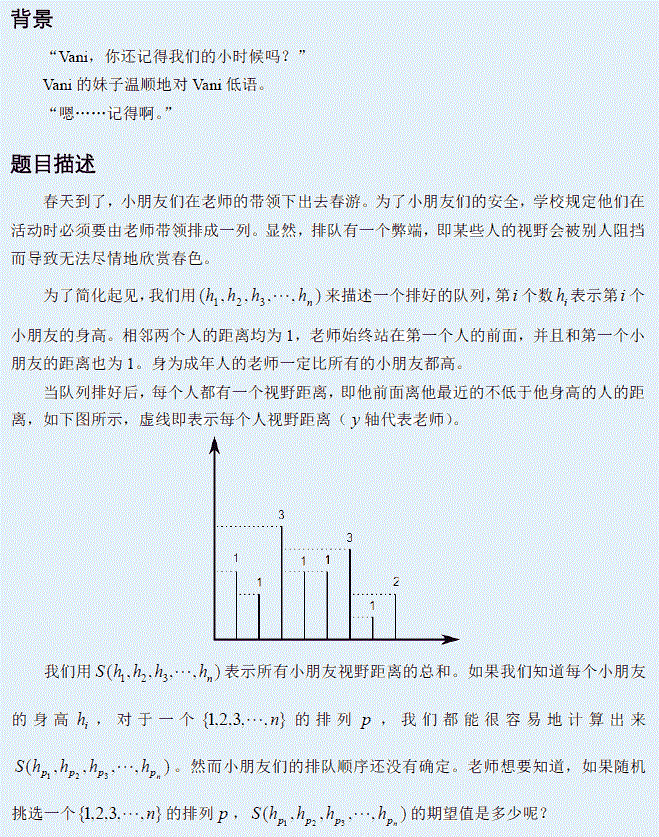（单身人士不可做

Input                     |            Output

3                                           |            4.33

1 2 3                                     |

Solutoin

---

1.O(n³)暴力算法：

无脑暴力可以枚举身高+位置+长度算期望再加和，O(n³)的复杂度，目测会T (所以根本没敢尝试

2.O(n²)优化算法：

然后会发现不同位置相同长度会产生很多重复计算，所以改为可以改为不枚举位置，直接计算每一长度的概率。

令s是比某小朋友身高矮的人数，那么对于长度l，该小朋友的概率为s/(n-1)*(s-1)/(n-2)...*(s-L+1)/(n-L)。 O(n²)解决。

3.O(n)数学算法:

最终答案为小朋友期望视野的总和，根据期望的线性性，答案可化为所有可能视野的期望值。即：

ans=∑i*p(l=i)      (i>=1且i<=n)可巧妙转化为

ans=∑p(l>=i)      (i>=1且i<=n)

对于p(l>=i)，令k为可能挡住当前小朋友的人数，考虑当前小朋友身前必须至少有i-1个比他矮的小朋友，因此他可站的位置有n-i+1个；k位挡视野的小朋友不能站在这i-1个位置，因此只能在剩下n-i个位置中选择。然后考虑小朋友自己和挡视野的人在n个位置中排列的合法情况，相除，就是p(l>=i)。

p(l>=i)=(n-i+1)*A(k,n-i)/A(k+1,n).

然后进行一通猛如虎的操作,最后可得一个神奇的O(1)式子。

p(l>=i)=(n+1)/(k+2).

具体推导过程见不认识的dalao的博客 传送门

---

O(n)的代码:

#include<bits/stdc++.h>
using namespace std;
int n,h[1001],k[1001];
double ans;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
void write(int x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x>9)
        write(x/10);
    putchar(x%10+'0');
}
int main()
{
    n=read();
    memset(k,-1,sizeof(k));
    for(int i=1;i<=n;i++)
    {
        int x=read();
        h[x]=h[x]+1;
    }
    for(int i=1;i<=1000;i++)
        for(int j=1;j<=i;j++)
            k[j]+=h[i];
    for(int i=1;i<=1000;i++)
        if(h[i])
            ans+=(double)h[i]*(n+1)/(k[i]+2);
    printf("%.2lf",ans);
    return 0;
}