五分钟带你读懂 堆 —— heap（内含JavaScript代码实现！！）

一、概念

 说起堆，我们就想起了土堆，把土堆起来，当我们要用土的时候，首先用到最上面的土。类似地，堆其实是一种优先队列，按照某种优先级将数字“堆”起来，每次取得时候从堆顶取。

 堆是一颗完全二叉树，其特点有如下几点：

 1.可以使用一维数组来表示。其中，第i个节点的父节点、子节点index如下：

  - parent(i) = (i - 1) / 2; (取整)

  - leftChild(i) = i * 2 + 1；

  - rightChild(i) = i * 2 + 2;

 2.堆中某个节点的值总是不大于（最小堆）或不小于（最大堆）其父节点的值

 注1：为什么可以用一维数组来表示堆，因为堆是一颗完全二叉树，可以通过下标计算获得其父子节点的下标

 注2：除了根节点外，其它节点的排序是未知的。（也就是说我们只知道最大or最小值是根节点的值，不知道其它节点的顺序）

二、上浮（shiftUp）和下沉（shiftDown）

1. 上浮（shiftUp）（以构建最小堆为例）

上浮操作就是，如果一个节点比它父节点小，则将它与父节点交换位置。这个节点在数组中的位置上升。

2. 下沉（shiftDown）

下沉操作就是，如果一个节点比它子节点大，那么它需要向下移动。称之为“下沉”。

三、堆的构建

给定一个一维数组[4,1,3,2,16,9,10,14,8,7]，怎么把它构建成一个堆呢？使用自底向上的方法将数组转化为堆。

大体思路为：如果每一个节点都是一个堆（以这个节点为根），那么这个数组肯定是一个堆。自底向上的方法意思就是，自底向上依次调整每个节点，使得以该节点为根的树是一个堆。

（以最大堆为例）

1. 首先将数组还原成一个完全二叉树
   
   、
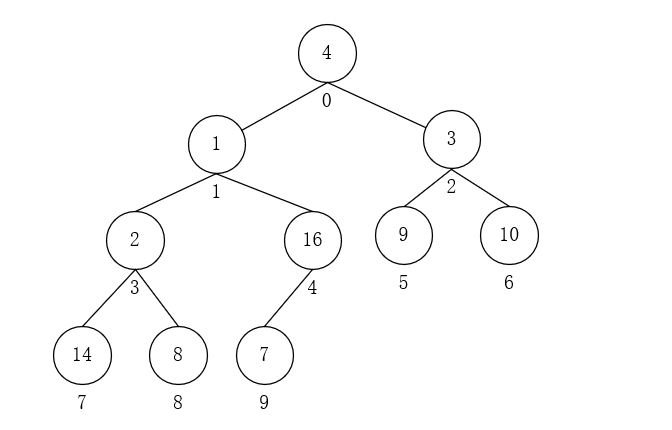2. 从倒数第一个非叶子节点开始（i = (n/2)-1，其中，n是数组的长度），依次对每个节点执行步骤3，将其调整成最大堆，直至第0个节点。
   
   注：这里要说一下为啥从第一个非叶子节点开始，因为叶节点没有孩子节点，可以把它看成只有一个元素的堆。
3. 将以第i个节点为根节点的子树调整为最大堆。假设根节点A[i]的左右子树的根节点index分别为left[i]和right[i]，其中，left[i]和right[i]都是最大堆。采用逐级下降的方法进行调整，具体步骤如下：
   
   （1） 从A[i]、A[left[i]]、A[right[i]]中找到最大的值，将其下标存到largest中。如果A[i]是最大的，那么以i为根节点的子树是最大堆；否则，交换A[i]和A[largest]的值。
   
   （2） 对下标为largest为根的子树重复（1）操作，直至largest为叶子节点。

 时间复杂度：O(n)

 （此推到过程以后有时间了再说，可以先记一下）

如图所示：

• 从 i = 4 开始遍历，此时，A[4] = 16，它是一个最大堆；
• i = 3，A[3] = 2，与A[7]交换，因为i = 7是叶子节点，所以调整完毕。
• i = 2，A[2] = 3，与A[6]交换，因为i = 6是叶子节点，所以调整完毕。此时，该树变成：
  
  
• i = 1，A[1] = 1，与A[4]交换。因为i = 4不是叶子节点，所以要对以4为根的子树进行上述操作；此时，A[4] = 1，与A[9]交换，i = 9是叶子节点，调整完毕。如下图所示：
  
  
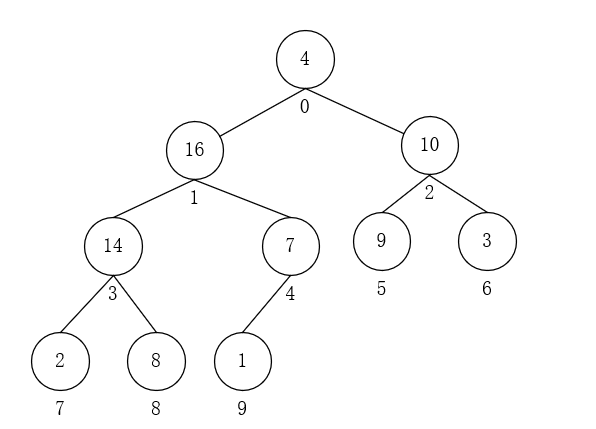
• i = 0，A[0] = 4，与A[1]交换。因为i = 1不是叶子节点，对以1为根的子树进行上述操作；此时，A[1] = 4，与A[3]交换，i = 3不是叶子节点，对以3为根的子树重复进行操作；此时A[3] = 4，与A[8]交换，i = 8是叶子节点，调整完毕。最终得到最大堆：
  
  

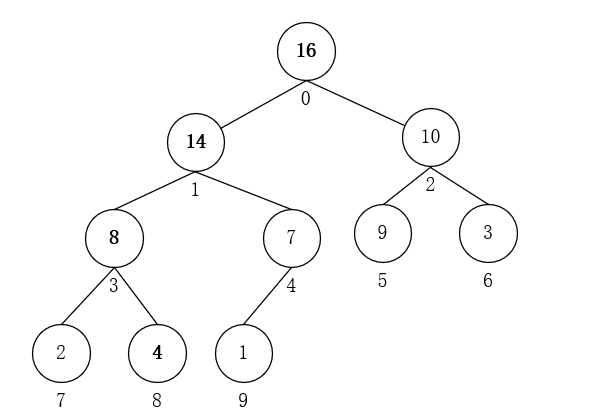
四、堆的其它方法

1.插入

向数组最后插入一个数据，然后再向上调整。还以上述数组为例，插入一个11。

• 在数组最后插入11
  
  
• 比较该节点与其父节点的大小，11 > 7，交换两者，进行上浮。重复该步骤，11 < 14，此时满足最大堆性质，插入完毕。
  
  

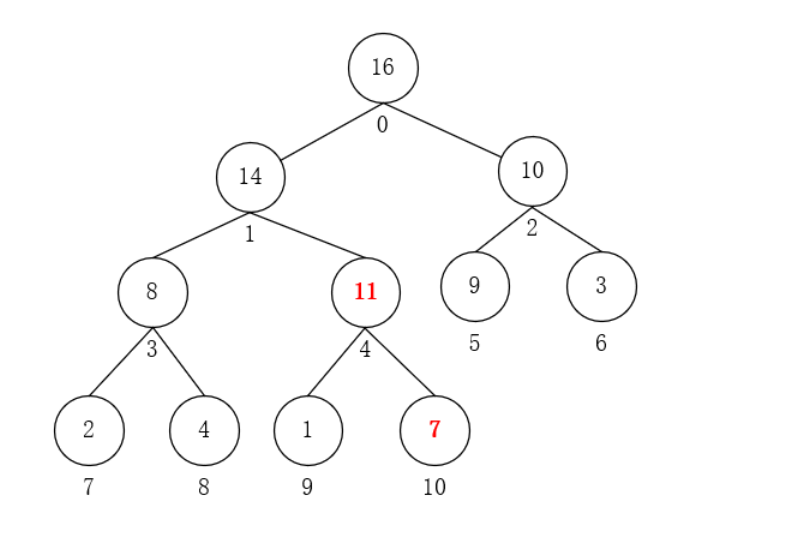
 时间复杂度：O(logn)

2.删除（指删除堆顶的数据）

交换堆顶和最后一个数据，删除最后一个数据，再对堆顶数据进行向下调整算法。

• 交换堆顶和最后一个数据，并删除最后一个数据。
  
  
• 堆根节点进行下沉操作：对比该节点和其左右子节点，将该节点与最大的节点进行交换。重复此操作，直至该节点为叶子节点。（因为这个节点原本就是叶子节点交换上去的，比上面所有层的节点都小，所以调整完毕后，这个节点一定仍是叶子节点）
  • 1与14交换
  • 1与8交换
  • 1与4交换
    
    

 时间复杂度：O(logn)

五、堆排序

基本思路：

• 将输入的数组建成最大堆。此时，堆顶元素就是最大值。
• 交换堆顶元素和末尾元素。此时，末尾元素是最大值。
• 将剩下 n-1 个元素重新构造成一个堆。重复执行上述步骤。

举个简单的例子：[14, 8, 10, 4]

1. 将该数组构建成最大堆
   
   
2. 交换堆顶元素和末尾元素。
   
   
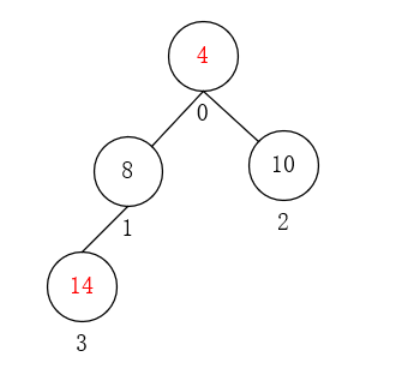
3. 忽略末尾元素，将剩下的元素利用下沉法重新构造为一个最大堆。
   
   
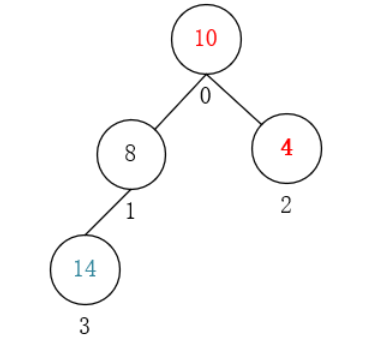
4. 重复以上步骤，直至剩下的元素只剩下一个。最终得到如下结果，排序完毕：
   
   

 时间复杂度：O(nlogn)

六、堆的应用

1. 优先队列（先填个坑，回头补上）

2. 求Top K

不管是面试还是啥，每次问到求Top K的问题，我们第一反应就是利用堆，但是怎么用呢？

Top K问题可抽象成两类，一类是针对静态数据集合，即数据是事先确定的；一类是针对动态数据集合，即数据动态地加入到集合中。

针对静态集合

维护一个大小为K的小顶堆，顺序遍历数组，从数组中取出数据与堆顶元素比较。如果比堆顶元素大，则把堆顶元素删除，并把该元素插入堆中；反之则不做处理，继续遍历数组。数组遍历完毕后，堆中的数据就是前K大数据了。

时间复杂度：O(nlogK)

针对动态集合

其实思路与静态集合大体一致，只不过静态集合是遍历数组，将数组中的元素与堆顶比较然后然后进行一系列操作；而动态集合是每加入一个元素，将该元素与堆顶比较，然后进行操作。

时间复杂度：O(logK)

七、JavaScript实现堆类

js中并没有“堆”这个数据结构，只能手动实现，以下是源代码。

class MaxHeap {
    constructor(heap) {
        this.heap = heap;
        this.heapSize = heap.length;
        this.buildMaxHeap();
    }

    // 构建最大堆
    buildMaxHeap() {
        for (let i = Math.floor(this.heapSize / 2) - 1; i >= 0; i--) {
            this.maxHeapify(i);
        }
    }

    //将以i为根节点的子树调整为最大堆
    maxHeapify(index) {
        let left = 2 * index + 1;
        let right = 2 * index + 2;
        let largest = index;
        if (left < this.heapSize && this.heap[left] > this.heap[largest]) largest = left;
        if (right < this.heapSize && this.heap[right] > this.heap[largest]) largest = right;
        if (largest !== index) {
            this.swapNum(index, largest);
            this.maxHeapify(largest);
        }
    }

    //交换i，j的值
    swapNum(i, j) {
        let temp = this.heap[i];
        this.heap[i] = this.heap[j];
        this.heap[j] = temp;
    }

    //插入一个数
    insert(num) {
        this.heap.push(num);
        this.heap.heapSize = this.heap.length;
        let index = this.heap.heapSize - 1;
        while (index != -1) {
            index = this.shiftUp(index);
        }
        console.log(this.heap);
    }

    //删除堆顶元素
    pop() {
        this.swapNum(0, this.heapSize - 1);
        this.heap.pop();
        this.heapSize = this.heap.length;
        let index = 0;
        while (1) {
            let temp = this.shiftDown(index);
            if (temp === index) break;
            else index = temp;
        }
    }

    //堆排序
    heapSort() {
        while (this.heapSize > 1) {
            this.swapNum(0, this.heapSize - 1);
            this.heapSize -= 1;
            let index = 0;
            while (1) {
                let temp = this.shiftDown(index);
                if (temp === index) break;
                else index = temp;
            }
        }
        this.heapSize = this.heap.length;
    }

    //上浮操作 - 将当前节点与父节点进行比较，如果该节点值大于父节点值，则进行交换。
    shiftUp(index) {
        let parent = Math.ceil(index / 2) - 1;
        if (this.heap[index] > this.heap[parent] && parent >= 0) {
            this.swapNum(index, parent);
            return parent;
        }
        return -1;
    }

    // 下沉操作 - 将当前节点与左右子节点进行比较，如果该节点值不是最大，则进行交换
    shiftDown(index) {
        let left = Math.floor(index * 2) + 1;
        let right = left + 1;
        let largest = index;
        if (left < this.heapSize && this.heap[left] > this.heap[largest]) largest = left;
        if (right < this.heapSize && this.heap[right] > this.heap[largest]) largest = right;
        if (largest !== index) {
            this.swapNum(index, largest);
        }
        return largest;
    }

}

八、参考文章：

1. 《算法导论第3版》
2. https://blog.csdn.net/qq_41754573/article/details/103371579
3. https://www.jianshu.com/p/6b526aa481b1