A pure L1-norm principal component analysis

@

目录

• 问题
• 细节
  • 的损失函数
  • 算法
    • 投影
    • 坐标系
    • 载荷向量

A pure L1-norm principal component analysis

虽然没有完全弄清楚其中的数学内涵，但是觉得有趣，记录一下.

问题

众所周知，一般的PCA(论文中以\(L_2-PCA\)表示)利用二范数构造损失函数并求解，但是有一个问题就是会对异常值非常敏感. 所以，已经有许多的PCA开始往\(\ell_1\)范数上靠了，不过我所知道的和这篇论文的有些不同.

像是Zou 06年的那篇SPCA中:



注意到，\(\ell_1\)作用在\(\beta\)上，以此来获得稀疏化.

这篇论文似乎有些不同，从回归的角度考虑, 一般的回归问题是最小化下列损失函数:

\[\sum_{i=1}^n (y_i - (\beta_0 + \mathbf{\beta}^Tx_i))^2.
\]

为了减小异常值的影响，改用:

\[\sum_{i=1}^n |y_i - (\beta_0 + \mathbf{\beta}^Tx_i)|.
\]

而作者指出，上面的问题可以利用线性规划求解:



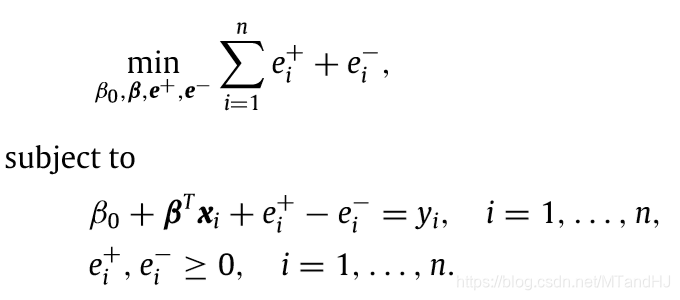
回到PCA上，我们希望找到一个方向，样本点到此方向上的\(\ell_1\)距离之和最短(可能理解有误的).

细节

\(L_1-PCA\)的损失函数

首先，假设输入的数据\(x_i \in \mathbb{R}^m\), 并构成数据矩阵\(X \in \mathbb{R}^{n \times m}\). 首先，作者希望找到一个\(m-1\)维的子空间，而样本点到此子空间的\(\ell_1\)距离和最短. 在此之前，需要先讨论距离的计算.

从上图可以看到，一个点到一个超平面\(S\)的\(\ell_1\)距离并不像普通的欧氏距离一样，实际上，可以这么定义点到子空间的距离:

\[d(x,S)=\inf \{\|x-z\|| \forall z \in S\}.
\]

假设超平面S由\(\beta^T x=0\)刻画(假设其经过原点), 则:

首先，对于一个样本点\(x_i\), 选择一个\(j\)， 令\(y_i=z_i, i = \not j\)， 而\(y_j\)定义为(假设\(\beta_j = \not 0\))：

\[-\frac{\sum_{i = \not j} \beta_i x_i}{\beta_j}
\]

于是容易证明\(\beta^T y=0\)， 也就是\(y \in S\).

下面证明， 如果这个\(j\)使得\(|\beta_j| \ge |\beta_i|, \forall i = \not j\), 那么\(|x-y|\)就是\(x\)的\(\ell_1\)距离. 首先证明，在只改变一个坐标的情况下是最小的, 此时:

\[|x-y| = |x_j+\frac{\sum_{i = \not j} \beta_i x_i}{\beta_j}|=|\frac{\sum_{i } \beta_i x_i}{\beta_j}|=\frac{|\beta^Tx|}{|\beta_j|}.
\]

因为分子是固定的，所以分母越大的距离越短，所以在只改变一个坐标的情况下是如此，下面再利用数学归纳法证明，如果距离最短，那么必须至多只有一个坐标被改变.

\(m=2\)的时候容易证明，假设\(m=k-1\)的时候已经成立，证明\(m=k\)也成立:

如果\(x, y\)已经存在一个坐标相同，那么根据前面的假设可以推得\(m=k\)成立，所以\(x, y\)必须每个坐标都完全不同. 不失一般性，选取\(\beta_1, \beta_2\)，且假设均不为0， 且\(|\beta_1| \le |\beta_2|\).

令\(y'_1=x_1, y'_2=y_2-\frac{\beta_1(x_1-y_1)}{\beta_2}\)，其余部分于\(y\)保持相同.则距离产生变化的部分为:

\[|x_1-y_1'|+|x_2-y_2'|=|y_2-x_2 - \frac{\beta_1(x_1-y_1)}{\beta_2}|\le |y_2-x_2|+|x_1-y_1|
\]

所以，新的\(y'\)有一个坐标相同，而且距离更短了，所以\(m=k\)也成立.

所以，我们的工作只需要找到最大\(|\beta_j|\)所对应的\(j\)即可.

所以，我们的损失函数为:

\[\sum_i \frac{|\beta^T x_i|}{|\beta_j|}.
\]

因为比例的关系，我们可以让\(\beta_j=-1\)而结果不变:

\[\sum_i |x_{ij}-\sum_{k = \not j}\beta_kx_{ik}|.
\]

把\(x_{ij}\)看成是\(y\)，那么上面就变成了一个\(\ell_1\)回归问题了. 当然我们并不知道\(j\)，所以需要进行\(m\)次运算，来找到\(j^*\)使得损失函数最小. 这样，我们就找到了一个\(m-1\)维的子空间.

算法如下:

\(L_1-PCA\)算法

因为PCA的目的是寻找一个方向，而不是一个子空间，所以需要不断重复寻找子空间的操作，这个地方我没怎么弄懂，不知是否是这样:

1. 找到了一个子空间
2. 将数据点投影到子空间上
3. 寻找新的坐标系，则数据会从\(k\)-->\(k-1\)维
4. 在新的数据中重复上面的操作直至\(k=1\).

有几个问题:

投影

对应算法的第4步，其中



需要一提的是，这里应该是作者的笔误，应当为:

\[(I_{j^* \ell}^{j^*})^m = \beta_{\ell}^m, \ell = \not j^*,
\]

理由有二:

首先，投影，那么至少要满足投影后的应当在子空间中才行，以3维样本为例:\(x=(x_1, x_2, x_3)^T, j=2\),

按照修改后的为:

\[z = (x_1, \beta_1x_1+\beta_3 x_3, x_3)
\]

于是\(\beta^Tz=0\), 而按照原先则不成立，

其次，再后续作者给出的例子中也可以发现，作者实际上也是按照修改后的公式进行计算的.

另外，提出一点对于这个投影方式的质疑. 因为找不到其理论部分，所以猜想作者是想按照\(\ell_1\)的方式进行投影，但是正如之前讲的，\(\ell_1\)的最短距离的投影是要选择\(|\beta_j|\)最大的\(j\)，而之前选择的\(j^*\)并不能保证这一点.

坐标系

论文中也有这么一段话.

既然\(\ell_1\)范数不具备旋转不变性，那么如何保证这种坐标系的选择是合适的呢，还有，这似乎也说明，我们最后选出来的方向应该不是全局最优的吧.

载荷向量

\(\alpha^k\)是第k个子空间的载荷向量，所以，所以和SPCA很大的一个区别是它并不是稀疏的.

另外，它还有一个性质，和由\(V^k\)张成的子空间正交，这点很好证明，因为\(Z^k\beta=0\).

总的来说，我觉得这个思想还是蛮有意思的，但是总觉得缺乏一点合理的解释，想当然的感觉...