[POJ 3150] Cellular Automaton (矩阵高速幂 + 矩阵乘法优化）

Cellular Automaton

Time Limit: 12000MS		Memory Limit: 65536K
Total Submissions: 3048		Accepted: 1227
Case Time Limit: 2000MS

Description

A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. Theorder
of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.

The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.

One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of orderm.
We will denote such kind of cellular automaton as n,m-automaton.

A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.

On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.

The following picture shows 1-step of the 5,3-automaton.

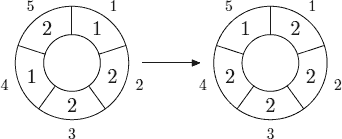
The problem is to calculate the state of the n,m-automaton after k d-steps.

Input

The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < ⁿ⁄₂ , 1 ≤ k ≤ 10 000 000). The second
line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.

Output

Output the values of the n,m-automaton’s cells after k d-steps.

Sample Input

sample input #1
5 3 1 1
1 2 2 1 2

sample input #2
5 3 1 10
1 2 2 1 2

Sample Output

sample output #1
2 2 2 2 1

sample output #2
2 0 0 2 2

Source

Northeastern Europe 2006

题目大意：

有一个环，长度为n。当中每个结点上面都有数字。能够对环上的每个结点进行更新，使得该结点的值变为环上距离该结点的距离小于等于d的全部节点数之和，最后再对m取模。每次操作更新一遍环上全部点，问经过k次操作之后，环上各点数字为多少。

解题思路：

　　首先能够想到用矩阵来取代操作。（对于题目第一组例子）

首先矩阵a = 1 2 2 1 2 

b = 

1 1 0 0 1

1 1 1 0 0

0 1 1 1 0

0 0 1 1 1

1 0 0 1 1

然后能够通过矩阵高速幂来解决。这样复杂度为（logk * n^3），会T。

事实上这个矩阵是有规律的。

b^1 =

[1, 1, 0, 0, 1]

[1, 1, 1, 0, 0]

[0, 1, 1, 1, 0]

[0, 0, 1, 1, 1]

[1, 0, 0, 1, 1]

b^2 =

[3, 2, 1, 1, 2]

[2, 3, 2, 1, 1]

[1, 2, 3, 2, 1]

[1, 1, 2, 3, 2]

[2, 1, 1, 2, 3]

b^3 =

[7, 6, 4, 4, 6]

[6, 7, 6, 4, 4]

[4, 6, 7, 6, 4]

[4, 4, 6, 7, 6]

[6, 4, 4, 6, 7]

b^4 =

[19, 17, 14, 14, 17]

[17, 19, 17, 14, 14]

[14, 17, 19, 17, 14]

[14, 14, 17, 19, 17]

[17, 14, 14, 17, 19]

观察能够发现，仅仅要把矩阵第i行的第一个数字移到最后，就变成了矩阵的第 i + 1 行。所以我们仅仅须要知道矩阵的某一行，就能够推得其它行。所以N^3的复杂度就将为N^2。

代码：

/*
ID: wuqi9395@126.com
PROG:
LANG: C++
*/
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<vector>
#include<string>
#include<fstream>
#include<cstring>
#include<ctype.h>
#include<iostream>
#include<algorithm>
#define INF (1<<30)
#define PI acos(-1.0)
#define mem(a, b) memset(a, b, sizeof(a))
#define For(i, n) for (int i = 0; i < n; i++)
typedef long long ll;
using namespace std;
const int maxn = 505;
const int maxm = 505;
int mod, n, k, d;
void Matrix_pow(int a[], int b[]) {
    ll c[505] = {0};
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) c[i] += ((ll)a[j] * b[(i + j) % n]) % mod;
        c[i] %= mod;
    }
    for (int i = 0; i < n; i++) b[i] = c[i];
}
int a[505], b[505];
int main () {
    while(scanf("%d%d%d%d", &n, &mod, &d, &k) != EOF) {
        for (int i = 0; i < n; i++) scanf("%d", b + i);
        memset(a, 0, sizeof(a));
        a[0] = 1;
        for (int i = 1; i <= d; i++) a[i] = a[n - i] = 1;
        while(k) {
            if (k & 1) Matrix_pow(a, b);
            k >>= 1;
            Matrix_pow(a, a);
        }
        for (int i = 0; i < n; i++) printf("%d%c", b[i], " \n"[i == n - 1]);
    }
    return 0;
}

參考：http://www.cppblog.com/varg-vikernes/archive/2011/02/08/139804.html