poj 2057 树形DP，数学期望

题目链接：http://poj.org/problem?id=2057

题意:有一只蜗牛爬上树睡着之后从树上掉下来,发现后面的"房子"却丢在了树上面, 现在这只蜗牛要求寻找它的房子,它又得从树根开始爬起,现在要求一条路径使得其找到房子
所要爬行的期望距离最小. 爬行距离如下计算, 题目规定每一个分支和枝末都看做是一个节点, 这些节点之间的距离都是1, 在分支上可能会有热心的毛毛虫, 这些毛毛虫会如实的告诉蜗牛他之前是否经过这条路径, 也正是因为毛毛虫, 因此询问毛毛虫的顺序使得这题的期望是不同的. 输入数据时给定的一个邻接关系,通过上一个节点来构图 ；同时字符 'Y'表示该点有毛毛虫, 字符'N'表示该点

分析：

die[i]表示以 i 为根结点找不到房子时要爬行的最少距离。

当 i 没有毛毛虫的时候  j 是 i 的子节点。

当 i 有毛毛虫的时候 ;

win[i]表示以 i 为根结点时，选好所有分支后，枚举完所有房子落在所有叶子结点的时候，要爬的最短距离。

就是说：当我走到 j 而找到时，前面的都失败了。而 j 成功了。j 子树 又有很多叶子结点。其中只有一个是成功的（并不知道是哪个）。

如图：

然后就是对于 i 结点来说，怎么访问才使得重复结点最少。

那就是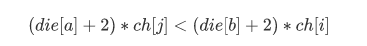 

 #include <cstdio>
 #include <iostream>
 #include <vector>
 #include <algorithm>
 #include <cstring>

 using namespace std;

 const int maxn = ;
 int pos[maxn];
 int snode[maxn];
 int die[maxn];
 int win[maxn];
 int n;

 vector<int>vec[maxn];

 void init()
 {
     memset(pos,,sizeof(pos));
     memset(snode,,sizeof(snode));
     memset(die,,sizeof(die));
     memset(win,,sizeof(win));

     char ps;
     int pre;
     for(int i=;i<=n;i++) {
         vec[i].clear();
     }

     for(int i=;i<=n;i++) {
         scanf("%d %c%*c",&pre,&ps);
         if(pre==-) continue;
         vec[pre].push_back(i);
         if(ps=='Y') pos[i] = ;
     }
 }

 int cmp(int a,int b) {
     return (die[a]+)*snode[b]<(die[b]+)*snode[a];
 }

 void dfs(int x) {
     int len  = vec[x].size();
     for(int i=;i<len;i++)
         dfs(vec[x][i]);
     if(len ==)
     {
         snode[x] = ;
         die[x] = ;
         win[x] = ;
         return;
     }
     for(int i=;i<len;i++) {
         snode[x] +=snode[vec[x][i]];
         if(pos[x]==) die[x] +=die[vec[x][i]] + ;
     }

     int tmp[];
     for(int i=;i<len;i++) {
         tmp[i] = vec[x][i];
     }

     int sum = ;
     sort(tmp,tmp+len,cmp);
     for(int i=;i<len;i++) {
         win[x] +=(sum+)*snode[tmp[i]] + win[tmp[i]];
         sum +=die[tmp[i]]+;
     }

 }

 int main()
 {
     while(scanf("%d%*c",&n),n) {
         init();
         double ans;
         dfs();
         ans = 1.0*win[]/snode[];
         printf("%.4lf\n",ans);
     }
     return ;
 }