数据结构学习-BST二叉查找树 ： 插入、删除、中序遍历、前序遍历、后序遍历、广度遍历、绘图

二叉查找树（Binary Search Tree）

是一种树形的存储数据的结构

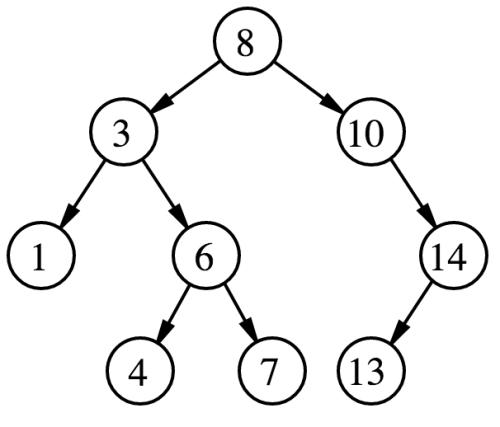
如图所示，它具有的特点是：

1、具有一个根节点

2、每个节点可能有0、1、2个分支

3、对于某个节点，他的左分支小于自身，自身小于右分支

接下来我们用c++来实现BST的封装

首先我们编写每个节点的类结构，分析可以知道我们每一个节点需要存储一个数据（data），左分支（left指向一个节点），右分支（right指向另一个节点）

因此我们建立

bstNode.h

#ifndef TEST1_BSTNODE_H
#define TEST1_BSTNODE_H
template <typename T> //这里使用模板类，以放入多种类型的数据，值得一提的是模板类不能讲声明和实现放在两个文件中
class bstNode{
public:
    T data;
    bstNode* left;
    bstNode* right;
    bstNode(){  //默认构造函数
        data = ;
        left = nullptr;
        right = nullptr;
    }
    bstNode(T val){   //赋值构造函数
        data = val;
        left = nullptr;
        right = nullptr;
    }
};
#endif //TEST1_BSTNODE_H

接下来我们创建封装了各种方法的树形结构类：

myBST.h

这个头文件的设计思路如下：

1、先包含bstNode* root作为根节点，在通过根节点的左右指针延伸出整棵树；

2、封装了一些会用到的方法：搜索指定值（Search）、找出一颗子树中的最小值（treeMin）、插入指定值（Insert）、删除指定值（Delete）、判断是否是叶子结点（isLeaf）、判断是否有两个孩子（isNodeWithTwoChild）、

三种遍历方式（前序PreorderTraversal、中序InorderTraversal、后序Postodertraversal）、删除所有节点（DeleteAllNodes）、广度搜索进行周游（BFTraversal）、横着画图（Graph）、返回根节点（getRoot）、判断树空（isEmpty）

默认构造函数、vector为参数的构造函数、数组和长度为参数的构造函数、析构函数。

注意在这里为了防止公有方法直接调用私有数据，采用了创建以"__"开头的私有方法，让公有方法先来调用该私有方法，再让私有方法来调用私有数据，以确保其安全性。

#ifndef TEST1_MYBST_H
#define TEST1_MYBST_H

#include <iomanip>
#include "bstNode.h"
#include <vector>
#include <deque>
#include <iostream>
using namespace std;

template <typename T>
class myBST{
private:
    bstNode<T> * root = nullptr;
    bstNode<T> * __search(bstNode<T> * root , const T &key){
        if (nullptr == root)
            return nullptr;
        if (key == root->data)
            return root;
        else if (key < root->data)
            return __search(root->left, key);
        else
            return __search(root->right, key);
    } //查找关键字是否存在
    bstNode<T> * __treeMin(bstNode<T> * root , bstNode<T> * &parent){
        bstNode<T> * curr = root;
        while(curr->left!= nullptr){
            parent = curr;
            curr = curr->left;
        }
        return  curr;
    } //返回最小节点（一路向左）
    bool __Insert(const T &key){
        bstNode<T> * temp = new bstNode<T>(key);
        bstNode<T> * parent = nullptr;
        if(isEmpty()){
            root=temp;
            return true;
        }
        else{
            bstNode<T> * curr;
            curr = root;
            while(curr){
                parent = curr;
                if(temp->data>curr->data) curr=curr->right;
                else curr = curr->left;
            }
            if(temp->data<parent->data){
                parent->left=temp;
                return true;
            }
            else {
                parent->right = temp;
                return true;
            }
        }
        return false;
    } //插入指定值
    bool __Delete(const T &key){
        bool found = false;//存储有没有找到key的变量
        if(isEmpty()){
            cerr<<"BST为空"<<endl;
            return false;
        }
        bstNode<T> * curr = root;
        bstNode<T> * parrent = nullptr;
        while(curr!= nullptr) {
            if (key == curr->data) {
                found = true;
                break;
            } else {
                parrent = curr;
                if (key < curr->data) curr = curr->left;
                else curr = curr->right;
            }
        }
        if(!found){
            cerr<<"未找到key！"<<endl;
            return false;
        }
        if (parrent == nullptr){//删除根节点
            root = nullptr;
            delete(curr);
            return true;
        }
        /*
         删除的节点有三种可能：
         1、叶子结点
         2、一个孩子的节点
         3、两个孩子的节点
         */
        if (__isLeaf(curr)){ //删除的点是叶子结点
            if(parrent->left==curr) parrent->left= nullptr;
            else parrent->right= nullptr;
            delete(curr);
            return true;
        }
        else if(__isNodeWithTwoChild(curr)){ //是两个孩子的节点
            //以当前右子树中的最小值取代他
            bstNode<T> * parrent = curr;
            bstNode<T> * tmp = __treeMin(curr->right,parrent);
            curr->data = tmp->data;
            if(parrent->right==tmp)
                parrent->right== nullptr;
            else parrent->left== nullptr;
            delete(tmp);
            return true;
        }
        else{ //只有一个孩子的节点
            if(curr->left!= nullptr){
                if(curr->left == curr){
                    parrent->left=curr->left;
                    delete(curr);
                    return true;
                }
                else{
                    parrent->right=curr->right;
                    delete(curr);
                    return true;
                }
            }
            if(curr->right!= nullptr){
                if(curr->left == curr){
                    parrent->left=curr->left;
                    delete(curr);
                    return true;
                }
                else{
                    parrent->right=curr->right;
                    delete(curr);
                    return true;
                }
            }
        }
        return false;
    } //删除指定值
    bool __isLeaf(bstNode<T> * const & root){
        if(root->left== nullptr && root->right== nullptr) return true;
        else return false;
    }//判断是否是叶子节点
    bool __isNodeWithTwoChild(bstNode<T> * const & root){
        if(root->left!= nullptr && root->right!= nullptr) return true;
        else return false;
    }//判断是否有两个孩子
    void __InorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        __InorderTraversal(root->left,result);
        cout<<root->data<<" ";
        result.push_back(root->data);
        __InorderTraversal(root->right,result);
    }//中序遍历
    void __PreorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        cout<<root->data<<" ";
        result.push_back(root->data);
        __InorderTraversal(root->left,result);
        __InorderTraversal(root->right,result);
    }//前序遍历
    void __PostorderTraversal(bstNode<T> *root,std::vector<int>&result){
        if(nullptr == root) return;
        __InorderTraversal(root->left,result);
        __InorderTraversal(root->right,result);
        cout<<root->data<<" ";
        result.push_back(root->data);
    }//后序遍历
    void __DeleteAllNodes(bstNode<T> *root){
        if (root == nullptr) return;
        __DeleteAllNodes(root->left);
        __DeleteAllNodes(root->right);
        __Delete(root->data);
    }//删除所有节点
    void __BFTraversal(vector<T>&result) {
        deque<bstNode<T> *> TQueue;
        bstNode<T> *pointer = root;
        if (pointer != nullptr) {
            TQueue.push_back(pointer);
        }
        while (!TQueue.empty()) {
            pointer = TQueue.front();
            TQueue.pop_front();
            cout << pointer->data << " ";
            result.push_back(pointer->data);
            if (pointer->left != nullptr) TQueue.push_back(pointer->left);
            if (pointer->right != nullptr) TQueue.push_back(pointer->right);
        }
    } //广度搜索来进行周游
    void __Graph(int indent,bstNode<T>* root){
        if(root != ){
            __Graph(indent + , root->right);
            cout<<setw(indent)<<" "<<root->data<<endl;
            __Graph(indent + , root->left);
        }
    } //横着画图的内部接口
    bstNode<T> * __GetRoot(){
        return root;
    } //返回根节点的内部接口
public:
    myBST(){
        root = nullptr;
    } //默认构造
    myBST(vector<T> arr){
        root = nullptr;
        for(int i =;i<(int)arr.size();i++){
            __Insert(arr[i]);
        }
    }
    myBST(T * arr,int len){
        root = nullptr;
        for(int i =;i<len;i++){
            __Insert(*(arr+i));
        }
    }
    ~myBST(){
        bstNode<T> * curr = root;
        __DeleteAllNodes(curr);
    }//析构
    bool isEmpty() const{
        return root == nullptr;
    }//判断树空
    bool search(const T &key){
        bstNode<T> * temp = __search(root, key);
        return (temp == nullptr) ? false : true;
    }//查找关键字是否存在的对外接口
    bool Insert(const T &key){
        return __Insert(key);
    }//插入节点的外部接口
    bool Delete(const T &key){
        return __Delete(key);
    }//删除节点的外部接口
    void InorderTraversal(vector<T>&result){
        __InorderTraversal(root, result);
    }//中序遍历的外部接口
    void PreorderTraversal(vector<T>&result){
        __PreorderTraversal(root, result);
    }//前序遍历的外部接口
    void PostorderTraversal(vector<T>&result){
        __PostorderTraversal(root, result);
    }//后序遍历的外部接口
    void BFTraversal(vector<T>&result){
        return __BFTraversal(result);
    } //广度搜索外部接口
    void Graph(int indent,bstNode<T>* root){
        return __Graph(indent,root);
    } //横着画图的外部接口
    bstNode<T> * GetRoot(){
        return __GetRoot();
    } //返回根节点的外部接口
};

#endif //TEST1_MYBST_H

最后来进行测试：

main.cpp

#include <iostream>
#include <vector>
#include "myBST.h"
#include "bstNode.h"
using namespace std;
int main() {
    vector<int> in = {,,,,,,,,,};
    myBST<int> bst(in);
    bst.Delete();
    bst.Insert();
    bool found = bst.search();
    if(!found)
        cout<<"not found!"<<endl;
    else
        cout<<"found!"<<endl;
    vector<int> result;
    cout<<"InorderTravelsal:  ";
    bst.InorderTraversal(result);
    cout<<endl<<"PreorderTravelsal:  ";
    bst.PreorderTraversal(result);
    cout<<endl<<"PostorderTraversal:  ";
    bst.PostorderTraversal(result);
    cout<<endl<<"BFTraversal:  ";
    bst.BFTraversal(result);
    cout<<endl<<"Graph:"<<endl;
    bstNode<int>* pointer = bst.GetRoot();
    bst.Graph(,pointer);
    return ;
}

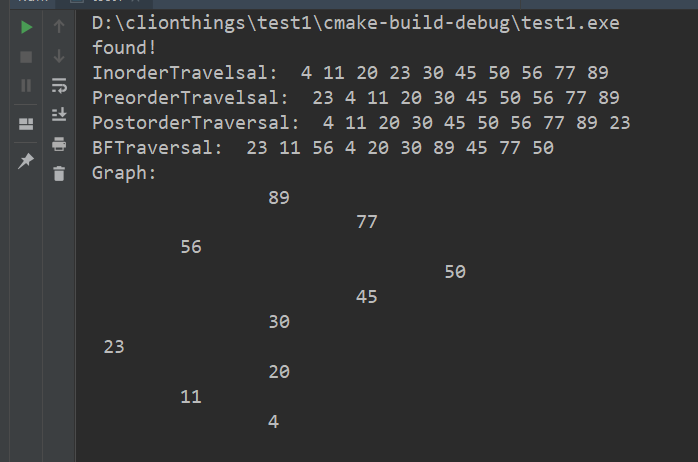
得到图示结果：

参考：https://blog.csdn.net/zhangxiao93/article/details/51444972