AVL旋转树

执行插入操作可能出现不平衡的情况，当平衡二叉树。AVL这树是一种自平衡二叉树，使二叉树又一次保持平衡。而且查找、插入和删除操作在平均和最坏情况下时间复杂度都是O(log n)

AVL树的旋转一共同拥有四种情形。注意全部旋转情况都是环绕着使得二叉树不平衡的第一个节点展开的。

1. LL型

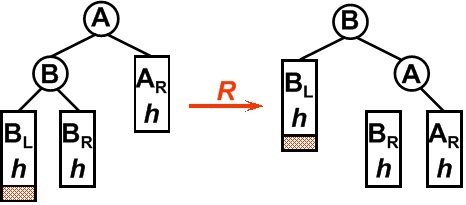
平衡二叉树某一节点的左孩子的左子树上插入一个新的节点，使得该节点不再平衡。这时仅仅须要把树向右旋转一次就可以，如图所看到的。原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树（图上忘在A于Brh之间标实线）

2. RR型

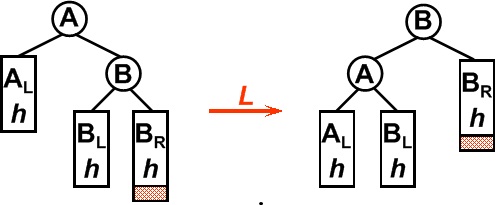
平衡二叉树某一节点的右孩子的右子树上插入一个新的节点，使得该节点不再平衡。这时仅仅须要把树向左旋转一次就可以。如图所看到的，原A右孩子B变为父结点。A变为其左孩子。而原B的左子树Blh将变为A的右子树。

3. LR型

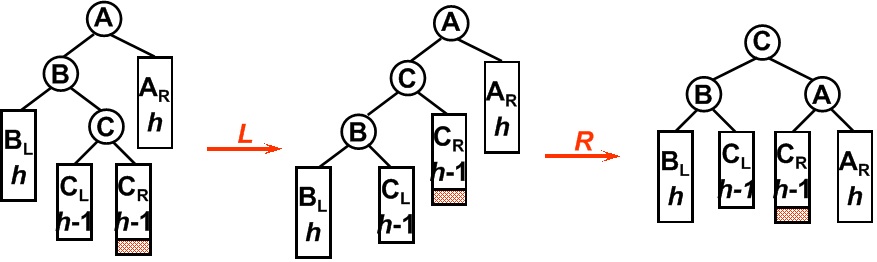
平衡二叉树某一节点的左孩子的右子树上插入一个新的节点。使得该节点不再平衡。这时须要旋转两次，仅一次的旋转是不可以使二叉树再次平衡。

如图所看到的，在B节点依照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还须要再向右旋转一次。

4. RL型

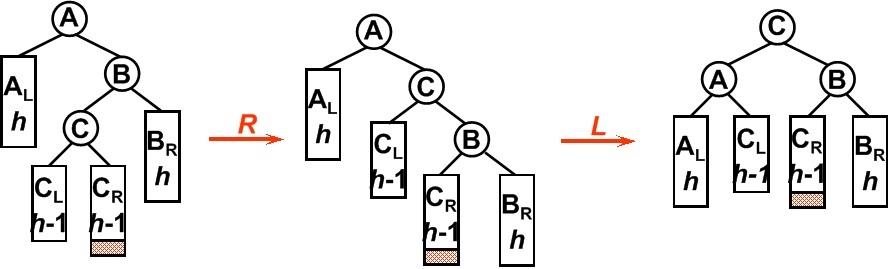
平衡二叉树某一节点的右孩子的左子树上插入一个新的节点，使得该节点不再平衡。

相同。这时须要旋转两次。旋转方向刚好同LR型相反。

版权声明：本文博主原创文章。博客，未经同意不得转载。