概率图模型&机器学习 -- 精确推断方法 -- 变量消去(Variable Elimination)和信念传播(Belief Propagation)

参考资料

• 西瓜书
• An introduction to hidden Markov model -- Rabiner, Juang
• 【机器学习】【白板推导系列】【合集 1～33】_哔哩哔哩_bilibili
• CS 228 - Probabilistic Graphical Models
• Max-product algorithm

Inference

推断就是在求各种概率。比如常见的：

• Marginal：假设随机变量\(x_1,...,x_n\) 和联合概率分布\(P(x_1,...,x_n)\)，求\(P(x_i)\).
• Conditional：\(P(Y\mid D)\), \(P(O_{1:k}\mid \lambda)\).

最基本的方法：用积分进行边际化、条件概率公式。

下面讨论精确推断方法。它们本质上都是动态规划方法，核心思想都是存储下子问题的结果，以克服重复计算。

Variable Elimination (VE, 变量消去法)

Motivation Example: Markov Chain

直接积分求边缘概率

根据概率图模型基础知识，该模型的联合概率密度\(P(a,b,c,d,e)\)可以写成：

\[P(a,b,c,d,e) = P(a)P(b\mid a)P(c\mid b)P(d\mid c) P(e\mid d)
\]

对于随机变量\(e\)，计算其边缘概率，可以对剩下几个随机变量求和：

\[P(e) = \sum_a\sum_b\sum_c\sum_d P(a)P(b\mid a)P(c\mid b)P(d\mid c) P(e\mid d)
\]

假设都是离散型随机变量，每个随机变量的取值\(a,b,c,d,e \in \{v_1,...,v_k\}\)，那么上述的边缘概率所需的计算量是\(k^4\) (只看循环).

更一般地，对于\(N\)个随机变量的马尔可夫链，每个随机变量的取值有\(K\)种，计算任一变量的边缘概率所需的时间复杂度是\(O(K^{N-1})\).

计算量比较大，因为直接积分的方法没有利用Markov Chain的结构性质。

用变量消去法简化运算

是一种很简单而且广泛使用的方法，核心思想：

• 理论基础：根据乘法分配律，调换求和的顺序。
• 目的：调换求和顺序后，可以进一步利用(图)模型描述的变量之间的关系来简化运算。

比如还是考虑上面的Markov Chain：

对于刚才的直接求和式子，调换一下顺序可以得到：

\[\begin{aligned}
P(e) &= \sum_a\sum_b\sum_c\sum_d P(a)P(b\mid a)P(c\mid b)P(d\mid c) P(e\mid d)\\
&= \sum_b\sum_c\sum_d P(c\mid b)P(d\mid c) P(e\mid d) \sum_aP(a)P(b\mid a) \\
\end{aligned}
\]

式子\(\sum_a P(a)P(b\mid a)\)相当于把\(a\)给积掉了，求了个对\(b\)的边缘概率，我们简写成\(\psi_a(b)\)代回上式：

\[\begin{aligned}
P(e) &= \sum_b\sum_c\sum_d P(c\mid b)P(d\mid c) P(e\mid d) \psi_a(b)
\end{aligned}
\]

这里可以看出计算量是如何减少的。本来是\(k^4\)次，现在只需要先计算出\(\psi_a(b)\)，然后再计算三层的和式，即只需要\(k^3 + k\)次计算。

还可以进一步调换循环顺序，把对\(c\)的边缘概率记作\(\psi_b(c)\)，则有：

\[\begin{aligned}
P(e)&= \sum_c\sum_d P(d\mid c) P(e\mid d) \sum_b P(c\mid b) \psi_a(b) \\
&= \sum_c\sum_d P(d\mid c) P(e\mid d) \psi_b(c)
\end{aligned}
\]

同理，现在只需要\(k^2 + 2k\)次计算。还可以继续把剩下的两个和式都消去，最后计算\(P(e)\)就只需要\(4k\)次计算了，指数复杂度简化成了多项式复杂度。

Example: Forward Algorithm

问题描述

考虑如下的隐马尔科夫模型 (HMM)：

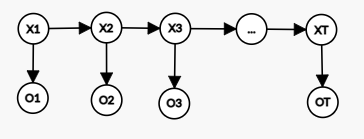
• 隐变量取值：\(X_t \in \{q_1, q_2,...,q_N\}\).
• 观测变量取值：\(O_t \in \{v_1,v_2,...,v_M\}\).
• 隐变量状态转移矩阵：\(a_{ij}=P(X_{t+1} = q_j \mid X_t = q_i)\).
• 观测变量概率分布：\(b_j(k) = P(O_t = v_k \mid X_t=q_j)\).
• 初始状态分布：\(\pi(X_1 = q_i) = P(X_1 = q_i)\).
  
  后三个是模型的参数，合并在一起时写作\(\lambda = <a,b,\pi>\).

问题：给定一段长度为\(T\)的观测序列\(O_{1:T} = \{O_1,...,O_T\}\)和模型\(\lambda\)，欲推断如下概率：

\[P(O_{1:T}\mid \lambda) = \sum_{\text{all } X_{1:T}} P(O_{1:T}, X_{1:T} \mid \lambda)
\]

问题转化

使用条件概率公式，再代入模型参数，上式可以转化为：

\[\begin{aligned}
P(O_{1:T} \mid \lambda) &= \sum_{\text{all } X_{1:T}} P(O_{1:T} \mid X_{1:T}, \lambda) P(X_{1:T}\mid \lambda) \\
&= \sum_{X_1,X_2...X_T} b_{X_1}(O_1)b_{X_2}(O_2)...b_{X_{T-1}}(O_T)~~\pi(X_1 = q_i)a_{X_1X_2}a_{X_2X_3}...a_{X_{T-1}X_T}
\end{aligned}
\]

和刚才的Markov Chain一样，要直接积分计算的话，需要枚举所有可能的隐变量取值，计算量非常大。

使用VE方法简化计算

同样也可以考虑调换求和顺序来化简：

\[\begin{aligned}
P(O_{1:T} \mid \lambda) &= \sum_{X_1,X_2...X_T} b_{X_1}(O_1)b_{X_2}(O_2)...b_{X_{T-1}}(O_T)~~\pi(X_1 = q_i)a_{X_1X_2}a_{X_2X_3}...a_{X_{T-1}X_T}\\
&=\sum_{X_{2:T}}...b_{X_2}(O_2)\sum_{X_1}\pi(X_1 = q_i) b_{X_1}(O_1) a_{X_1X_2}
\end{aligned}
\]

像在Markov Chain里那样，定义\(\psi(X_2) = \sum_{X_1}\pi(X_1 = q_i) b_{X_1}(O_1) a_{X_1X_2}\)，可以进一步化简：

\[\begin{aligned}
P(O_{1:T} \mid \lambda) &= \sum_{X_2...X_T} b_{X_2}(O_2)...b_{X_{T-1}}(O_T)~~\psi(X_2)a_{X_2X_3}...a_{X_{T-1}X_T} \\
&=\sum_{X_3...X_T}...b_{X_3}(O_3)\sum_{X_2}\psi(X_2)b_{X_2}(O_2) a_{X_2X_3}
\end{aligned}
\]

一步一步化简下去，计算量会大大减少。

使用前向算法递推计算

下面是前向算法的一般化描述，之后会尝试说明前向算法就是变量消去法。

首先定义：

\[\alpha_t(i) = P(O_{1:t}, X_t = q_i \mid \lambda)
\]

容易知道\(P(O_{1:T}\mid \lambda)= \sum_{i=1}^N \alpha_T(i) = \sum_{X_T} P(O_{1:T}, X_T \mid \lambda)\).

\(\alpha_t(i)\)表示的是前\(t\)次观测为\(O_{1:t}\)，并且在\(t\)时刻的隐状态\(X_t = q_i\)的概率。可以用递推的方式求解：

1. \(\alpha_1(i) = \pi(X_1=q_i)b_{q_i}(O_1)\).
2. \(\alpha_{t+1}(j) = [\sum_1^N \alpha_t(i)a_{ij}]b_j(O_{t+1})\), \(1\le j \le N\).
   
   要直接理解这个递推式非常容易：\(\alpha_t(i)\)乘\(a_{ij}\)得到\(P(O_{1:t},X_t = q_i,X_{t+1}=q_j\mid \lambda)\)，再做边际化，消去了\(X_t\)就得到\(P(O_{1:t},X_{t+1}=q_j\mid \lambda)\)，最后乘上\(b_j(O_{t+1})=P(O_{t+1}\mid X_{t+1}=q_j)\)，就得到了\(\alpha_{t+1}(j)\).

前向算法就是VE方法

把\(\alpha\)代入到上面的变量消去过程来进一步理解：

\[\begin{aligned}
P(O_{1:T} \mid \lambda) &= \sum_{X_1,X_2...X_T} b_{X_1}(O_1)b_{X_2}(O_2)...b_{X_{T-1}}(O_T)~~\pi(X_1 = q_i)a_{X_1X_2}a_{X_2X_3}...a_{X_{T-1}X_T}\\
&=\sum_{X_{2:T}}...b_{X_2}(O_2)\sum_{X_1}\pi(X_1 = q_i) b_{X_1}(O_1) a_{X_1X_2}\\
&=\sum_{X_{2:T}}...b_{X_2}(O_2) \sum_{i=1}^N \alpha_1(i) a_{iX_2}
\end{aligned}
\]

用VE方法更换求和顺序，再把\(\alpha\)代入后，得到了和前向算法递推式一样的形式，这就说明了前向算法其实就是一种变量消去法。

Belief Propagation -- Sum-product

Motivation: 变量消去法中的重复计算

考虑上方无向图模型，进行因子分解可得：

\[P(a,b,c,d,e) = \frac{1}{Z}\phi(a,b)\phi(b,c)\phi(c,d)\phi(c,e)
\]

其中\(Z\)是规范化因子 (之后省略不写)。考虑计算\(P(c)\)和\(P(b)\)，利用变量消去法，可以写出：

\[\begin{aligned}
P(c) &= \sum_a\sum_b\sum_e\sum_d \phi(a,b)\phi(b,c)\phi(c,d)\phi(c,e)\\
&= \sum_b\phi(b,c)\sum_a\phi(a,b) \sum_d \phi(c,d) \sum_e \phi(c,e)\\
&= \sum_b \phi(b,c)m_{ab}(b)m_{dc}(c)m_{ec}(c)\\
&= m_{abc}(c)m_{dc}(c)m_{ec}(c)
\end{aligned}
\]

\[\begin{aligned}
P(b) &= \sum_a\sum_c\sum_d\sum_e \phi(a,b)\phi(b,c)\phi(c,d)\phi(c,e)\\
&=\sum_a\phi(a,b) \sum_c \phi(b,c)\sum_d\phi(c,d)\sum_e \phi(c,e)\\
&=m_{ab}(b) \sum_c\phi(b,c) m_{dc}(c) m_{ec}(c)\\
&=m_{ab}(b) m_{dcb \text{ and }ecb}(b)
\end{aligned}
\]

这里把求和之后的式子用\(m\)来简单表示，下标表示计算过来的路径。

很容易可以看出重复计算的部分，比如\(m_{dc}(c)\)和\(m_{ec}(c)\)，在求\(P(c)\)的时候算了一次，求\(P(b)\)的时候又算了一次。

Sum-product

一个很自然的想法是在求边缘概率之前，把所有的\(m\)都先计算出来，减少冗余计算。信念传播算法给出了一种计算树形概率图的所有\(m\)的方法。

Sum-product第一步：Collect Message，算法会先任意选择一个点作为根节点，然后进行树的后序遍历，信息从叶子向根节点更新。对于任意节点\(u\)，假设父节点是\(p\)，子节点的集合是\(\text{son}(u)\)，计算从节点\(u\)到父节点\(p\)的\(m\)值，可以看作是从\(u\)向\(p\)传播了一次信息，计算方法如下：

\[m_{up}(p)= \sum_u \psi(u,p) \prod_{v \in \text{son(u)}} m_{vu}(u)
\]

比方说刚才的无向图例子中，如果选择\(b\)作为根节点，在collect message步计算\(m_{cb}(c)\) (或者表示成\(m_{dcb\text{ and }ecb}(c)\)) ：

\[m_{cb}(b)= \sum_c\phi(b,c)m_{dc}(c)m_{ec}(c)
\]

Sum-product第二步：Distribute Message，现在还只是求出了一个方向的信息，即从叶子节点到根节点的信息，还需要一次遍历，这一次把信息从根节点向叶子节点更新。树结构中，每个节点只会有一个父亲节点，这个性质使得distribute比collect容易 (所以下面用下标\(\text{root}\to u\)，和\(p\to u\)表示的是一个意思)：

\[m_{\text{root}\to u}(u) = \sum_p \psi(p,u) m_{\text{root}\to p}(p)
\]

再回到刚才的无向图例子中，如果选择\(a\)作为根节点，在distribute步计算\(m_{ac}(c)\)：

\[m_{ac}(c) = \sum_b\phi(b,c)\sum_a\phi(a,b) = \sum_b \phi(b,c) m_{ab}(b)
\]

---

这两个步骤之后，需要计算任意一个随机变量的边缘概率都会很容易：

\[P(u) = \prod_{v\in \text{neighbors(u)}} m_{vu}(u)
\]

Belief Propagation -- Max-product

最大边缘概率

假设随机变量集合\(X=\{x_1,...,x_n\}\)，定义最大边缘概率为：

\[P^*(x_i) = \max_{X\backslash x_i} P(x_1,...,x_n)
\]

显然，求出最大边缘概率后，再求一个最大值就可以算出最大联合概率：

\[P^* = \max P(x_1,...,x_n) = \max_{x_i} P^*(x_i)
\]

Max运算的分配律

在VE那部分提到一个重要的理论基础：乘法分配律。更准确地说，应该是乘法对加法的分配律 (multiplication distributes over addition).

实际上，当因子都是非负的时候 (概率图模型的因子分解刚好就是如此)，乘法对max运算也有分配律。因此，要求最大边缘概率 (或者最大联合概率) 时，可以用max运算来做变量消去。

再次考虑Sum-product章节中的无向图模型，以下使用VE方法分别化简了边缘概率和最大边缘概率：

\[\begin{aligned}
P(c) &= \sum_a\sum_b\sum_e\sum_d \phi(a,b)\phi(b,c)\phi(c,d)\phi(c,e)\\
&= \sum_b\phi(b,c)\sum_a\phi(a,b) \sum_d \phi(c,d) \sum_e \phi(c,e)\\
\end{aligned}
\]

\[\begin{aligned}
P^*(c) &= \max_{a,b,d,e} P(a,b,c,d,e) \\
&= \max_{a,b,d,e} \phi(a,b)\phi(b,c)\phi(c,d)\phi(c,e) \\
&= \max_b \phi(b,c) \max_a\phi(a,b) \max_d \phi(c,d) \max_e \phi(c,e)
\end{aligned}
\]

两者形式完全一样， 求max运算也可以看作是一次信息传递过程。所以，很自然地想到把信赖传播方法扩展到求最大边缘概率上。

BP -- Max-product

只需要把Sum-product中的求和符号改成\(\max\)即可：

\[m_{up}(p)= \max_u \psi(u,p) \prod_{\text{v=son(u)}} m_{vu}(u)
\]

• 如果问题只是要求\(\max P(x_1,...,x_n)\)，则只需要Collect message一次遍历就够了，不需要再distribute.
• 如果要求\(X^* = \arg \max_{X} P(X)\)，则只需要在每次传播信息的过程中，记录下每个\(\arg \max_u\)即可。